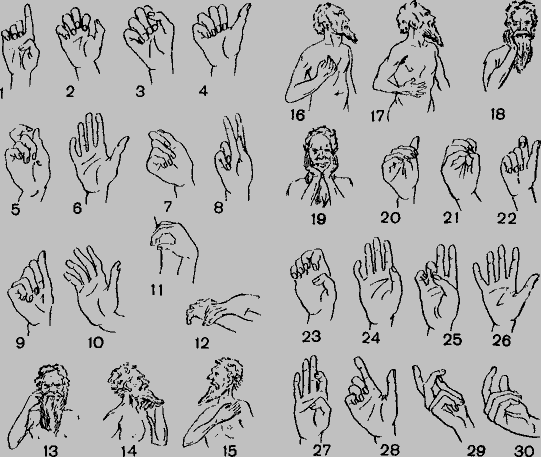
Общечеловеческим способом счета являются жесты рук, обозначающие числа (рис. 24). Счет на пальцах у всех первобытных народов предшествует числительным устного языка, что отражается и в происхождении самих числительных. Во многих языках, например в африканских (зулусский и другие языки банту), числительные обозначают только действия над пальцами рук. Языки могут различаться лишь конкретными операциями счета: «семь» может означать или «согни два пальца» (на второй руке): 7 = 5 + 2 или «согни в обратную сторону 3 пальца»: 7 = 10 − 3. Исследование числительных позволяет углубиться в такую предысторию культуры, когда «ручные понятия» были необходимыми хотя бы для первобытной арифметики у всех народов.
Изучая в поведении (в том числе и бессознательном) современного человека «окаменелые» пережитки древних систем знаков, Л. С. Выготский в качестве одного из наиболее ярких примеров приводит «рудиментарную форму культурной арифметики: счет на пальцах», который обнаруживается, в частности, в поведении ребенка. В своей современной форме счет на пальцах связан с левым полушарием. Так объясняется то, что при одних и тех же поражениях этого полушария обнаруживается и расстройство счета, и неузнавание собственных пальцев, входящие в так называемый синдром Герстмана.
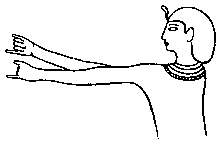
Самое раннее упоминание счета на пальцах в магическом значении содержится в древнеегипетском заклинании для получения перевоза. Умерший царь уговаривает перевозчика (подобного греческому Харону) дать ему переправиться на восточную сторону канала в потустороннем мире. На это перевозчик ему говорит: «Величественный бог на другой стороне скажет: не привел ли ты мне человека, который не может сосчитать свои пальцы?». Но царь в ответ читает стихотворение, каждая из строк которого соответствует одному из пальцев, расположенных в соответствии с египетским счетом (см. таблицу). Когда совершался магический счет, руки держались ладонями вверх, счет велся от большого пальца правой руки до большого пальца левой руки (см. таблицу) Отдельные жесты такого рода встречаются и на египетских изображениях (рис. 25).
| Древнеегипетский счет на пальцах | ||
| Палец | Рука | |
| Левая | Правая | |
| Большой | 1 | 10 |
| Указательный | 2 | 9 |
| Средний | 3 | 8 |
| Безымянный | 4 | 7 |
| Мизинец | 5 | 6 |
В культурах Древнего Востока уже отчетливо видно и другое проявление общечеловеческого стремления обозначать числа посредством иероглифов. В таких письменностях, как хеттская клинопись, было возможно написание чисел либо числительными, записанными (как многие другие слова) слоговыми фонетическими знаками, либо знаками-иероглифами. При этом почти всегда предпочитался второй способ.
Подобно тому, как счет на, пальцах долго сохраняется в качестве пережитка «ручных понятий», сочетающегося со звуковым языком, обозначение чисел письменными знаками-иероглифами (наряду с фонетической их записью числительными естественного языка) остается как пережиток в современных письменных европейских языках. Его сохранению, несомненно, способствует и практическое удобство сокращенной — посредством иероглифов — записи часто повторяющихся длинных сочетаний числительных. Когда мы записываем «три» как 3 или III, проявляется особый характер обозначений чисел, тяготеющих к иероглифам (и тем самым к сфере влияния правого полушария; к ней, вероятно, относились когда-то и жесты, из которых позднее развился пальцевый счет, перешедший в число операций, находящихся в ведении левого полушария).
Есть основания видеть ранние следы пальцевого счета и в самой ранней иероглифической «письменности» человечества — знаках и зарубках, сделанных человеком каменного века. Детальный анализ этих знаков палеолита, данный недавно Б. А. Фроловым, привел его к выводу, что в них особенно выделяются группы по 5 и 10 знаков, следовательно, с помощью таких зарубок человек фиксировал результаты сосчитанного по пальцам. Поэтому ошибались те историки математики, которые после открытия первых таких зарубок поспешно решили, будто счет с помощью зарубок предшествовал счету по пальцам.
Хронологически появление счета с использованием древнейших знаков письменности палеолита намного предшествует знакомству европейской науки с аборигенами Австралии, считавшими только по пальцам (без зарубок). Но культурное развитие человечества нельзя выстраивать по прямой линии сплошного прогресса. Средневековую науку в этом смысле можно уподобить афатику, который вновь обращается к счету по пальцам, утратив более современные способы счета В средние века для исчисления новолуний (в связи с которым, по мнению некоторых исследователей, возник развитый счет уже в палеолите) в Европе снова стал использоваться счет по пальцам. Но это не противоречит наличию до этого великих достижений греческой математики, как и еще более древних открытий. Углубленное изучение письменности палеолита не опровергает, а, скорее, подтверждает исключительную древность пальцевого счета, уходящего в предысторию Homo sapiens.
Счет по пальцам в его примитивной форме, предшествовавшей появлению числительных, мог быть связан, как и все системы жестов-иероглифов, с правым полушарием мозга. В пользу этого говорят свидетельства о счете на пальцах у таких австралийских племен, в чьем звуковом языке не было числительных больше «двух»: до четырех считали, повторяя слова «один» и «два», а дальше считали только по пальцам. Австралиец из подобного племени был отдан в школу европейского типа, он обучился считать до 20, но члены его племени остались безучастными к этому открытию, не имеющему никаких практических приложений. Тогда призадумался и юный австралиец: «Зачем было выучивать, что 8 + 9 = 17, если у меня нет стольких пальцев?».
Такая установка только на сиюминутную реальность, вообще типичная для «правого мозга», работающего в режиме реального времени, легко объяснима по отношению к явлениям, для обозначения которых существуют только знаки-иероглифы, которыми ведает правый мозг. Но даже и у тех индейцев Северной Америки, у которых в их устных языках есть числительные до 80, сохраняется сходная установка. Один из таких индейцев по просьбе ученых сосчитал только до 10 и добавил, что потом «ничего больше нет». Он привык пересчитывать только нечто реальное и осязаемое. Следовательно, даже и тогда, когда числа могут обозначаться словами естественного языка, по отношению к ним сохраняется установка, характерная для правого мозга, а не для левого.