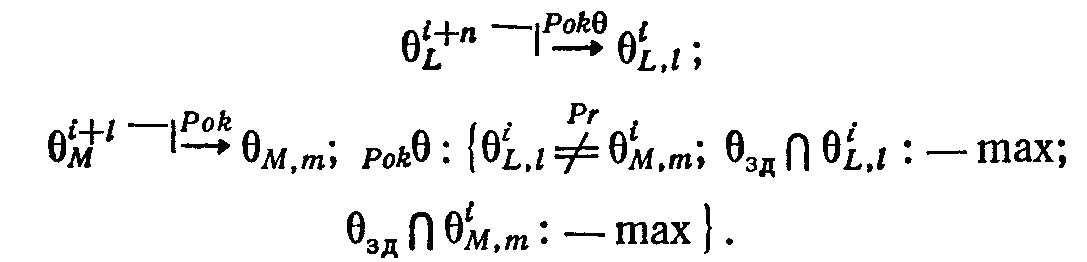Рассмотренный нами выше путь выбора элементов, тесно связанный с развитием учения И. П. Павлова, обеспечил преодоление ограничений, свойственних математике. Он базировался на основных положениях диалектического материализма о наличии причинно-следственных отношений и на теории отражения как основы информационной деятельности.
Возник вопрос: удастся ли использовать вновь созданную абстрактную систему так же эффективно, как это имело место ранее в области развития химии? Если бы удалось выявить общие законы и явления, определяющие функционирование любых информационных систем работы мозга, то поставленные цели исследования можно было бы считать достигнутыми. Тогда оказалось бы оправданным исключение из рассмотрения конкретных свойств систем рефлексов. В противном случае попытка была бы оценена как одна из ошибок в исследовании.
Поясним на хорошо известном всем примере развития и применения геометрии, что можно ожидать от использования абстрактной системы. Нам кажется привычным, что при рассмотрении формы предметов используются такие понятия, как линия, точка, квадрат, куб, прямоугольник. Однако до тех пор, пока эти идеальные объекты не были определены в области абстрактной теории — геометрии, решить вопросы, связанные с анализом формы предметов, например расчета площадей, было весьма трудно. Теперь, когда в рамках общей теории были сформулированы законы, описаны новые явления, возникающие в сложных системах, положение изменилось. В том случае, когда перед человеком возникают новые проблемы (например, связанные с анализом фермы предметов), достаточно описать реальные объекты и явления внешнего мира, новые задачи на языке абстрактной теории, в частности опознать в них наличие квадрата, куба, треугольника, шара.
Поскольку в области теории уже определены привила, законы, то установление соответствия между реальными объектами исследования и идеальными конструкциями приводит к возможности выявления новых свойств рассматриваемых объектов реального мира и решения относящихся к ним задач, в частности задачи расчета площадей, объемов. На идеальных моделях возможно проведение теоретического рассмотрения принципов организации более сложных систем, установление возникающих в них новых явлений, доказательство теорем. Теория обеспечивает возможность анализа работы сложных систем.
Можно ли рассчитывать на то, что абстракция, используемая при изучении информационных процессов работы мозга, приведет к подобным результатам? Удастся ли на основе представления реальных процессов на абстрактном языке теоретически вывести свойства более сложных информационных систем, а затем обнаружить их существование в реальных явлениях внешнего мира? Можно ли найти законы и описать новые свойства, которые имеют общее, универсальное значение? Удастся ли анализировать новые сложные формы информационной деятельности на основе обнаружения в них уже известных конструкций и описания объекта на языке теории? Окажется ли возможным на основе ранее уже установленных правил и законов, типов конструкций и законов их взаимодействия обнаружить в исследуемом объекте то, что не удавалось выявить ранее, или такая сложная система, как мозг человека, отличается от всего, что до сих пор знала наука?
Ответы на эти вопросы на первых этапах исследования не были однозначными. С одной стороны, были получены положительные результаты в изучении новых механизмов, с другой — не удалось решить задачи полной расшифровки механизмов сложных форм работы мозга, таких, например, как способность к самостоятельной постановке задач, к формированию новых алгоритмов.
Анализ возникающих трудностей привел Н. В. Целкову к выводу о необходимости построения абстрактной системы еще более высокого уровня. Мы говорили выше, о том, что идеализация первой категории привела к рассмотрению абстрактных информационных структур различных видов. Было высказано предположение о возможности и целесообразности исключить из рассмотрения конкретную организацию таких структур. Был введен символ , который обозначает структуру любого вида, и определены операции над такими символами. Операция в частности, означает процесс «порождения» структурой более высокого уровня абстракции множества конструкций более низкого уровня. Символы означают уровни
структуры. Символпозволяет отличить одну структуру от другой. Примеров таких операций можно привести очень много. Так, любой закон в области физики может быть по-разному интерпретирован при создании различных конкретных приборов, математическая формула может быть применена для различных конкретных расчетов и т. д. Все эти примеры кажутся непохожими друг на друга. При изучении мышления было важно исключить из рассмотрения специфику частных примеров и иметь возможность изучать «порождения новых частных интерпретаций» как таковое.
Операция заполнения одной из информационных структур пустых мест (локусов), включенных в другую структуру, обозначается Можно привести много примеров для иллюстрации этой системы отношений. Так, при решении математических задач имеет место подстановка конкретных чисел в формулу. При построении новой абстрактной системы II категории из таких отношений строятся композиции. Например, была сформулирована структура II категории следующего типа: из двух структур более высокого уровня строятся такие частные интерпретации которые не имеют противоречивых участков и в наибольшей степени удовлетворяют заданным критериям Такие комплексные системы отношений определялись формулой
Важно подчеркнуть, что поскольку символозначал любую из информационных структур I категории, то все выводы, сделанные на основании рассмотрения таких схем II категории, приобретали общее значение. Они должны были оказаться справедливыми при изучении любых алгоритмов и информационных механизмов.
При рассмотрении описываемых структур II категории возникал вопрос, удастся ли при их изучении выявить какие-либо существенные новые свойства и закономерности. Мы видели, что такие абстрактные системы исключали возможность рассмотрения алгоритмов и информационных механизмов и оказывались непригодными для решения многих актуальных проблем. В то же время, если бы удалось обнаружить в таких конструкциях новые в качественном отношении явления и законы, можно было бы вывести многие частные закономерности. Потеряв в области рассмотрения отдельных алгоритмов, исследователи приобрели бы возможность решать другую, не менее важную проблему раскрытия механизмов создания новых алгоритмов и информационных механизмов при работе мозга.