Офлайн А-Б тесты в ресторанах фастфуда. Часть 1: Планирование и верификация офлайн A-B-тестов

“Основа надёжного A/B — не магия формул, а понимание, с чего вы стартуете и с чем работаете.“

Привет! Меня зовут Елена Малая, я занимаюсь офлайн A/B-тестами в Бургер Кинг Россия.

В последнее время всё больше пишут про офлайн-эксперименты — и это здорово. Но мне часто не хватало материалов, приближённых к реальности: когда данных мало, шум высокий, а каждый тест — как разведоперация.

Эта статья — о том, как я выстраивала методологию A/B-тестирования в условиях офлайн-ритейла. Она для тех, кто работает с данными не в идеальном вакууме, а на земле — в ресторанах, ритейле, логистике.

Здесь не будет учебных формул — только рабочие подходы, предостережения и лайфхаки, собранные через тесты, ошибки и (маленькие) победы. Если вы, как и я, когда-то поняли, что “по книжке” оно не взлетает — welcome.

Есть мнение, что когда мало наблюдений, то искать там статистическую значимость бесполезно и применять теорию А/Б тестирования на практике нет смысла. Но, кто ищет тот всегда найдет :)), есть много методик, позволяющих снизить дисперсию вашей целевой метрики и в любом случае применение продвинутых методик поднимет уровень ваших А/Б тестов на новый уровень, выводы будут прозрачнее и логичнее и даже когда нету статистической значимости из-за недостаточности данных будет больше уверенности в результатах.

Погружаясь в мир математики А/Б тестирования понимаешь, что теория и обучение основывается на классическом рандомном делении выборки на группы, можно улучшать рандом, применять его разные виды, такие как полный, блочный или парный и далее работать с классическим А/Б тестом не беспокоясь о смещении выборок, которое может привести к ложным выводам. Когда же приходишь с этими «правильными» знаниями в реальный мир офлайн бизнеса картинка рушится. Начинаешь серфить по Интернету в поисках, хотя бы какой то, теории и чьего-то опыта. Понимаешь, что твои А/Б тесты, они как бы вовсе и не А/Б тесты, а causal inference, о котором уже гораздо меньше информации и почти нет обучения.

Специфика данных. У вас так же?

Для того чтобы погрузится в данные нужно сначала понять, что такое для наших офлайн А/Б тестов единица наблюдения? В нашем случае это ресторан/день. Очевидно, что каждый ресторан имеет свою региональную специфику, обязательно есть сезонность, операционные трудности приводят к временным остановкам работы ресторанов, сокращение меню, реставрации, отдаленные регионы, большая дисперсия, куча выбросов………и много важных для бизнеса идей, которые обязательно хочется протестировать.

Остановимся немного на особенностях офлайн-тестов:

Реальная физическая среда. Эксперименты проводятся в реальных точках, где на результаты влияют локальные факторы (расположение, окружающая инфраструктура, погодные условия, местные события).

Ограниченное кол-во наблюдений. Наблюдение это ресто/день, на тест выделяется небольшое кол-во ресторанов.

Сложности рандомизации. В отличие от онлайн, где пользователи автоматически и случайным образом распределяются между вариантами, в офлайн-тестах приходится заранее выделять тестовую группу (далее ТГ), прибегая к фильтрам и затем подбирать по определенному алгоритму контрольную группу (далее КГ). При этом нужно учитывать, что мы работаем с ресторанами, которых не много и они могут сильно отличаться друг от друга по поведению.

Логистическая сложность. Внедрение изменений в офлайн-точках может потребовать дополнительной подготовки (обучение персонала, настройка оборудования), что увеличивает временные и ресурсные затраты.

Какие же отличия от онлайн A/B-тестов:

Масштаб и скорость. Онлайн-тесты охватывают огромное количество пользователей и позволяют получать данные в реальном времени, тогда как офлайн-тесты ограничены числом физических точек и имеют более медленный сбор данных.

Контроль переменных. Онлайн-эксперименты легче контролировать — алгоритмы могут автоматически распределять пользователей и минимизировать влияние посторонних факторов. В офлайн условиях множество внешних факторов (местоположение, сезонность, местные события) усложняют контроль и интерпретацию результатов.

Сбор и обработка данных. Данные онлайн собираются автоматически и оперативно, что позволяет быстро корректировать эксперимент. В офлайн-тестах сбор данных часто требует дополнительных усилий, что может задерживать анализ.

Но, мы верим, что у нас все получится, поэтому продолжим :))

Бургер Кинг по России имеет немного меньше 1000 собственных ресторанов. При этом мы же понимаем все особенности, а значит нужно проверить наши рестораны на здоровье. Для всех параметры здоровья данных будут свои, для нас же это непрерывность трафика, когда у ресторана есть стабильные ежедневные продажи и это отсутствие очень большой волатильности в данных, когда слишком много выбросов.

Для оценки выбросов мы используем классический подход на основе межквартильного размаха (IQR):

Где:

• — первый квартиль (25%)

• — третий квартиль (75%)

• — межквартильный размах

Значения, выходящие за границы, считаются аномальными.

Если их доля превышает заданный порог (например, 5%), ресторан исключается из выборки ресторанов, которая далее распределяется на АБ тесты. Кроме того, мы также проверяем: статус ресторана (работал ли он в период анализа), непрерывность продаж и трафика, гомогенность дисперсий по дням (через непараметрические тесты), а также рассчитываем обобщённую категорию качества на основе пропусков, дисперсий и выбросов. Эти фильтры позволяют отсечь нерепрезентативные наблюдения ещё до подбора ТГ и КГ.

Таким нехитрым подходом мы сокращаем исходную выборку на X%. При этом важно помнить, что отобранные рестораны еще предстоит разделить на две группы — тестовую и контрольную. В данной статье я намеренно не акцентируюсь на методах формирования этих групп (например, методах мэтчинга или балансировки), поскольку считаю, что этой теме стоит посвятить отдельный материал. Отмечу лишь, что мы используем мэтчинг как один из наиболее устойчивых подходов. Отличный обзор по теме представлен, например, в статье X5 Tech «Методы балансировки в А/Б тестировании» — в ней хорошо раскрыты преимущества и ограничения различных методов. Основной фокус этой статьи — на проверке корректности полученного деления: насколько группы действительно сопоставимы, можно ли их валидно сравнивать, и как оценить устойчивость результатов A/A и A/B-тестов.

Вернемся к нашему процессу, проанализировав прогноз возможности такого подбора, наша выборка сократилась еще на Y%. А теперь стало грустно…Но,

Как же справляться с такими ограничениями?

Так как цель моей статьи структурировать подход и предложить рабочий вариант пред и пост анализа для таких данных я пройдусь по порядку, чтобы все было лаконично и последовательно.

Пару слов о дизайне, имея ограниченное количество ресторанов, мы понимаем, что в онлайн режиме невозможно выделять группы ресторанов на каждый запрос. В этом случае всегда кто-то будет обделен, тот кто придет первый запросит такое количество тестов, что на последующих просто не хватит ресторанов, контроль и оптимизация процесса определения максимального количества ячеек для ТГ будет затруднена. Поэтому мы определяем какое максимальное количество тестов мы можем провести в определенный промежуток времени, чтобы никого не обидеть и не допустить пересечения не ортогональных тестов.

Дизайн теста

Оформление заявки на A/B-тест: почему это важно и как избежать ошибок.

Итак, определено кол-во ячеек на тесты, почти все все запросы удовлетворены, готовимся к старту тестов. В этом разделе хочу затронуть оформление заявки на А/Б тест, кажется, что это просто, но отсутствие правил и шаблонов может запутать или упустить важное. Грамотное оформление заявки на A/B-тест важно, так как оно задаёт четкие цели, критерии и методику эксперимента, обеспечивая прозрачность и минимизируя ошибки при запуске и анализе результатов. Ниже пример стандартных пунктов, которые должны быть описаны в любой заявке на тестирование. Если ваши заказчики A/B-тестов ещё не привыкли к такому формату, сейчас — лучшее время познакомить их с корректным оформлением заявок. Это поможет сделать эксперименты более точными, а их результаты — более достоверными.

После согласования корректности заявки содержанию, выделенным срокам и выбранной целевой метрике (далее ЦМ) проводится работа в несколько этапов: 1. Перед стартом теста подбираются аналоги и проводится пред анализ, 2. Осуществляется контроль запуска теста на стороне заказчика, 3. Мониторинг промежуточных результатов для отслеживания технических проблем, 4. Пост анализ, 5. Обратная связь от заказчика по решениям теста.

Дальше подробнее остановимся на пунктах 1 и 4.

Немного теории об mde, ошибках I и II рода и размере выборки.

Так как в таблице выше есть параметры размера выборки и mde считаю, что необходимо немного рассказать о них. Сильно погружаться в математику не буду, потому что уже много статей, книг и обучения есть на эту тему. Для тех, кто «на этом уже собаку съел», предлагаю пропустить этот блок.

Гипотеза:
Четкое предположение о том, как изменение повлияет на ключевые метрики.
Пример: «Изменение меню увеличит средний чек на 5%.»

Минимальный детектируемый эффект (MDE):
Минимальное изменение, которое должно произойти, чтобы мы могли сказать, что результат не случаен.

•       Если эффект меньше MDE, это может быть статистической погрешностью.

•       Важно: заранее определить, какое изменение будет для нас значимым.

Уровень значимости (α):
Риск ошибочно заключить, что изменение сработало (ложноположительный результат).

•       Чем меньше α, тем выше уверенность, что результат не случайный.

•       Обычно α = 5%.

Мощность теста и риск β:
Риск пропустить реально работающие изменения (ложноотрицательный результат).

•       Чем меньше β, тем меньше шанс упустить полезное изменение.

•       Обычно мощность теста = 80% (β = 20%).

Продолжительность и размер выборки:
Зависят от выбранных α, β и MDE. Чем строже параметры – тем больше данных нужно собрать. Зависимость размера выборки от α, β и MDE предполагает нормальное распределение данных. В офлайн-тестах, где данные часто асимметричны или имеют выбросы, мы дополняем расчёты бутстрапом.

От чего еще зависит размер выборки? – влияние изменчивости данных.

Высокая изменчивость («шум»):

Примеры:

Клики на кнопку: Среднее ~50, но варьируется от 10 до 100

Средний чек: Среднее ~1000 руб., разброс от 500 до 5000 руб.

Следствие: для «вылавливания» сигнала требуется большая выборка, чтобы истинное изменение не «потерялось» в разбросе.

Низкая изменчивость:

Пример:

Скорость загрузки страницы: Среднее ~2 сек., колебания ±0.1 сек.

Следствие: менее «шумные» данные позволяют увидеть эффект даже при меньшем размере выборки.

Вывод: Размер выборки определяется не только уровнем α, β и MDE, но и степенью изменчивости данных. Чем выше разброс, тем больше наблюдений необходимо для достижения статистической значимости.

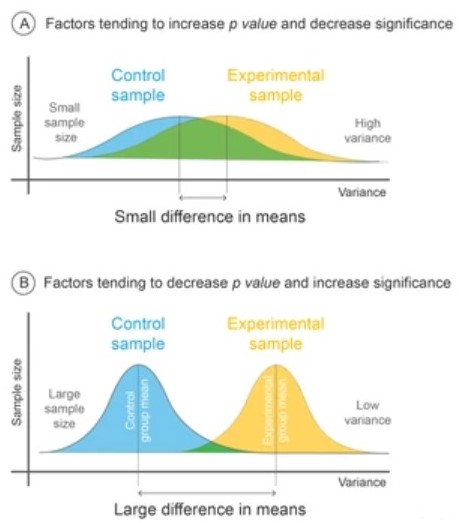
Когда будете анализировать размер выборки, рекомендую делать расчет зависимости размера выборки от эффекта и уровней ошибок I и II рода. Он может выглядеть так:

def get_sample_size_abs(epsilon, std, alpha=0.05, beta=0.2):
    t_alpha = norm.ppf(1 - alpha / 2, loc=0, scale=1)
    t_beta = norm.ppf(1 - beta, loc=0, scale=1)
    z_scores_sum_squared = (t_alpha + t_beta) ** 2
    sample_size = int(
        np.ceil(
            z_scores_sum_squared * (2 * std ** 2) / (epsilon ** 2)
        )
    )
    return sample_size
######################################################################
def get_sample_size_arb(mu, std, eff=1.01, alpha=0.05, beta=0.2):
    epsilon = (eff - 1) * mu
    return get_sample_size_abs(epsilon, std=std, alpha=alpha, beta=beta)
######################################################################
def get_table_sample_size(mu, std, effects, alphas, betas):
    results = []
    for eff in effects:
        results_eff = []
        for alpha in alphas:
            row = []
            for beta in betas:
                row.append(
                    get_sample_size_arb(
                        mu,
                        std,
                        eff=eff,
                        alpha=alpha,
                        beta=beta
                    )
                )
            results_eff.append(row)
        results.append(results_eff)

    # Создаем DataFrame
    df_results = pd.DataFrame(
        np.array(results).reshape(len(effects), len(alphas) * len(betas)),
        index=[f'{np.round((x - 1)*100, 1)}%' for x in effects],
        columns=pd.MultiIndex.from_product(
            [alphas, betas], names=["alpha", "beta"]
        )
    )
    return df_results
######################################################################
effects = np.linspace(1.01, 1.1, 10)  # Эффекты от 1% до 10%
alphas = [0.01, 0.05, 0.1]  # Разные уровни alpha
betas = [0.1, 0.2, 0.3]  # Разные уровни beta

mu = df['ЦМ'].mean()
std = df['ЦМ'].std()

table = get_table_sample_size(mu, std, effects, alphas, betas)
print(table)

Здесь же хочу упомянуть об интересном параметре Cohen’s, который можно будет применить в пост анализе. Параметр Cohen’s d используется для оценки размера эффекта в A/B-тестировании, позволяя понять, насколько значимо отличается среднее значение между двумя группами. Это помогает не только выявить статистически значимые различия, но и оценить их практическую значимость. Формула расчета параметра:

О параметре Cohen’s d редко пишут в контексте A/B-тестирования, потому что чаще акцент делают на статистической значимости (p-value) и доверительных интервалах. Многие фокусируются на “да/нет” результатах, упуская из виду размер эффекта, хотя он важен для понимания реального влияния изменений.

Предварительный анализ

Осуществив подбор контрольной группы (КГ) ресторанов к заранее выбранной тестовой группе (ТГ) выбранным методом, необходимо провести верификацию. Это важно, поскольку подбор был не случайным, а искусственным — в отличие от рандомизации, где факторы, влияющие на результат, распределяются равномерно.

Верификация позволяет убедиться, что КГ и ТГ сопоставимы по ключевым метрикам, таким как исторические данные по выручке, средний чек, количество посетителей и другие релевантные показатели. Это снижает риск искажений в результатах теста и повышает его достоверность.

Любой анализ данных начинается с визуализации — она помогает сразу выявить возможные проблемы и понять структуру данных.

Гистограмма и плотность распределения ЦМ

Гистограмма и KDE помогают визуально сравнить метрики в A/B-тесте. Гистограмма показывает частоту значений, а KDE — сглаженную вероятность. Эти графики помогают заметить выбросы, асимметрию или многомодальность распределения, что может повлиять на выбор статистических тестов.

Дополнительно можно использовать:

• Ящик с усами (Boxplot) — показывает медиану, квартили и выбросы.

• Кумулятивную функцию распределения (CDF) — для сравнения распределений двух групп.

• График квантиль-квантиль (Q-Q plot) — проверяет, насколько данные соответствуют заданному распределению.

Эти методы дают более полное представление о данных перед проведением статистических тестов.

plt.figure(figsize = (14, 6))
plt.subplot(121)
df_tg.target.hist(edgecolor='white', density = False, bins=50, alpha = 0.5, color='red') 
df_cg. target.hist(edgecolor='white', density = False, bins=50, alpha = 0.5)
plt.ylabel('Частота')
plt.xlabel('target')
# строим график плотности распределения
plt.subplot(122)
sns.kdeplot(df_tg. target, shade=True, legend=True, color='red')
sns.kdeplot(df_cg. target, shade=True, legend=True)
plt.xlabel(' target ')
plt.suptitle('Distribution of target', size=20);
# ящик с усами
sns.boxplot(data=df_channel, x='group', y=' target ');
plt.title("Boxplot");
# кумулятивная функция распредления
sns.histplot(x='target', data=dfl, hue='group', bins=len(df_channel), stat="density",
      element="step", fill=False, cumulative=True, common_norm=False);
plt.title("Cumulative distribution function");
# график квантиль-квантиль.
income = df[' target '].values
income_t = df.loc[df.group =='test', 'target'].values
income_c = df.loc[df.group=='control', ' target '].values

df_pct = pd.DataFrame()
df_pct['q_test'] = np.percentile(income_t, range(100))
df_pct['q_control'] = np.percentile(income_c, range(100))

plt.figure(figsize=(5, 5))
plt.scatter(x='q_control', y='q_test', data=df_pct, label='Actual fit');
sns.lineplot(x='q_control', y='q_control', data=df_pct, color='r', label='Line of perfect fit');
plt.xlabel('Quantile of income, control group')
plt.ylabel('Quantile of income, test group')
plt.legend()
plt.title("QQ plot");

Однако визуализации недостаточно — нам нужно статистически подтвердить корректность подбора КГ к ТГ. Для этого используется набор тестов, которые проверяют однородность распределений и отсутствие систематических различий между группами.

Тест Колмогорова – Смирнова.

В A/B-тестировании КС-тест проверяет, совпадают ли распределения метрики в контрольной и тестовой группах до старта эксперимента. Он сравнивает их эмпирические функции распределения (CDF) и измеряет максимальное отклонение между ними. Если p-value < 0.05, группы неоднородны — это сигнал пересобрать КГ или отменить тест. КС-тест полезен для сложных метрик без нормального распределения. Нужно упомянуть, что КС-тест чувствителен к размеру выборки: при больших выборках даже малые различия дают низкое p-value, а при малых он может быть недостаточно мощен. Поэтому мы дополняем его PSI.

from scipy.stats import ks_2samp
ks_2samp(df_tg.target df_cg.target)

Равенство средних.

Этот тест проверяет, отличаются ли средние значения метрики (например, выручки) между КГ и ТГ. Используется t-тест Стьюдента, который сравнивает две независимые выборки и оценивает, могли ли наблюдаемые различия возникнуть случайно.

from scipy.stats import ttest_ind
stat, p_value = ttest_ind(income_c, income_t)
print(f"t-test: statistic={stat:.4f}, p-value={p_value:.4f}")

Если p-value < 0.05, различия между группами статистически значимы, и подбор КГ стоит пересмотреть. Если p-value > 0.05, средние значения не различаются, что подтверждает корректность подбора.

Population Stability Index (PSI)

PSI используется для оценки стабильности распределений между КГ и ТГ. Он показывает, насколько сильно изменилась структура данных, и помогает выявить скрытые различия, которые не заметны при проверке только средних значений.

Интерпретация PSI:

• < 0.1 — группы почти идентичны, распределение стабильное.

• 0.1 – 0.25 — умеренные различия, возможны небольшие смещения.

• > 0.25 — значительные различия, группы несопоставимы.

Если PSI выше 0.25, подбор КГ стоит пересмотреть, так как такие различия могут исказить результаты A/B-теста.

def calculate_psi(test_data, control_data, bins=10):
    # Создаем бин границы на основе контрольных данных
    breakpoints = np.linspace(min(control_data), max(control_data), bins + 1)
    
    # Подсчитываем количество наблюдений в каждом бине для теста и контроля
    test_counts = np.histogram(test_data, bins=breakpoints)[0]
    control_counts = np.histogram(control_data, bins=breakpoints)[0]
    
    # Рассчитываем долю наблюдений в каждом бине
    test_pct = test_counts / len(test_data)
    control_pct = control_counts / len(control_data)
    
    # Заменяем нули маленькими значениями, чтобы избежать деления на ноль
    test_pct = np.where(test_pct == 0, 0.0001, test_pct)
    control_pct = np.where(control_pct == 0, 0.0001, control_pct)
    
    # Расчет PSI для каждого бина
    psi_values = (test_pct - control_pct) * np.log(test_pct / control_pct)
    
    # Возвращаем итоговое значение PSI
    psi = np.sum(psi_values)
    return psi

# Применяем на твоих данных
psi_value = calculate_psi(df_tg['target'], df_cg['target'], bins=10)
print(f'PSI: {psi_value}')

Корреляция ЦМ

Для балансировки контрольной (КГ) и тестовой групп (ТГ) в A/B-тестировании важным этапом верификации является анализ корреляции целевой метрики (ЦМ) между ними. Даже при качественном матчинге распределение ЦМ может оставаться несбалансированным, что влияет на корректность эксперимента. Высокая корреляция подтверждает сопоставимость групп не только по признакам, но и по ключевой метрике, снижая риск получения искажённых результатов. Низкая корреляция, напротив, может указывать на перекос в выборке, пропущенные ковариаты или ошибки в подборе соответствий, что ставит под сомнение достоверность выводов

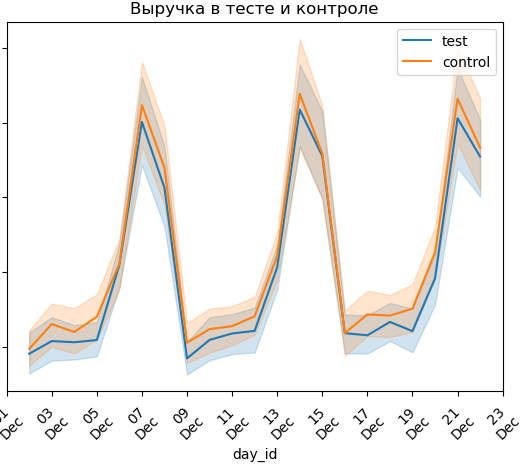
Анализ корреляции особенно важен перед запуском теста и при интерпретации результатов. Если после старта эксперимента корреляция резко меняется, это может свидетельствовать как о влиянии тестируемого воздействия, так и о скрытых факторах. Для оценки используют коэффициенты Пирсона или Спирмена, визуализируют распределение значений и сравнивают изменения до и после матчинга. Если выявлены отклонения, стоит пересмотреть методику сопоставления и проверить балансировку по ключевым признакам. Такой подход помогает минимизировать ошибки и повысить достоверность A/B-теста.

# график
day1=df.day_id.max()
fig, ax = plt.subplots()
sns.lineplot(x="day_id", y=" target ",data=df.query("group=='test' and day_id<=@day1"),label='test');
sns.lineplot(x="day_id", y=" target ",data=df.query("group=='control' and day_id<=@day1"),label='control');
plt.title(' target в тесте и контроле');

y_min = 0
y_max = df. target.mean() + df. target.std() * 3

ticker = mdates.DayLocator(interval=2)
ax.xaxis.set_major_locator(ticker)
dtFrmt = mdates.DateFormatter('%dn%b')
ax.xaxis.set_major_formatter(dtFrmt)
plt.xticks(rotation=45);
plt.legend(loc='upper right')
# формула
df_tg_gp = df_tg.groupby(['day_id'], as_index = False).agg({' target': 'mean'})
df_cg_gp = df_cg.groupby(['day_id'], as_index = False).agg({' target': 'mean'})

from scipy.stats import pearsonr
from scipy.stats import spearmanr
result0 = pearsonr(df_tg_gp.target, df_cg_gp.target)
print(' target Pearsons correlation:', result0)
result1 = scipy.stats.spearmanr(df_tg_gp.target, df_cg_gp.target)
print('GP spearmanr correlation:', result1)

Тест Манна–Уитни как финальная проверка эквивалентности распределений

На завершающем этапе верификации контрольной (КГ) и тестовой (ТГ) групп важно убедиться, что различия в распределении целевой метрики не выходят за рамки случайных флуктуаций. Для этого используется тест Манна–Уитни, который позволяет оценить, различаются ли распределения ЦМ в двух группах, даже если они имеют одинаковое среднее значение.

В отличие от классического t-теста, который чувствителен к выбросам и предполагает нормальность распределения, тест Манна–Уитни не требует этих условий, что делает его более устойчивым для эмпирических данных. Если p-value оказывается выше порогового значения (обычно 0.05), можно считать, что распределения ЦМ в КГ и ТГ не имеют значимых различий. В противном случае возможно наличие скрытых факторов или недостатков матчинга, что требует пересмотра состава групп.

Этот тест служит финальным барьером перед запуском эксперимента, позволяя убедиться, что группы действительно эквивалентны не только по среднему значению, но и по форме распределения. Его применение снижает вероятность искажений, вызванных некорректной балансировкой, и повышает надёжность результатов теста.

from scipy.stats import mannwhitneyu

test_group = df[df['group'] == 'test']['target']
control_group = df[df['group'] == 'control']['target']

stat, p_value = mannwhitneyu(test_group, control_group, alternative='two-sided')
print(f'Статистика Манна-Уитни: {stat:.4f}')
print(f'P-значение: {p_value:.4f}')
if p_value < 0.05:
    print("Гипотеза о равенстве распределений отвергается: есть значимые различия.")
else:
    print("Распределения эквивалентны: значимых различий нет.")

# Выполняем тест снова, но с возвращением рангов
stat, p_value = mannwhitneyu(test_group, control_group, alternative='two-sided')
print(f'Статистика U: {stat}')
print(f'P-значение: {p_value}')

# Вычисляем средние ранги вручную
combined = np.concatenate([test_group, control_group])
ranks = stats.rankdata(combined)
ranks_test = ranks[:len(test_group)]
ranks_control = ranks[len(test_group):]

mean_rank_test = np.mean(ranks_test)
mean_rank_control = np.mean(ranks_control)

print(f'Средний ранг тестовой группы: {mean_rank_test}')
print(f'Средний ранг контрольной группы: {mean_rank_control}')

Итоги верификации:

т-тест показал, что у выборок по целевой метрике средние равны,

Тест Колмогорова-Смирнова показал, что выборки исходят из одного распределения,

Индекс PSI показал отсутствие различий в выборках

Тест Манна–Уитни показал отсутствие различия

Корреляционный анализ: target Pearsons correlation: >0.95 (тут желательно добавить еще несколько ключевых влияющих метрик для контроля)

Подобный подход к верификации данных использует не только наша компания, Avito.tech, видео «Как мы запускали новую модель продвижения – матчинг и региональные тесты».

В этой части мы разобрали специфику офлайн-экспериментов, особенности подготовки данных и ключевые принципы верификации тестовой и контрольной групп. Мы убедились, что корректный дизайн и предварительная проверка — это не просто формальность, а основа надёжного A/B-тестирования.

Однако даже при идеально подобранных группах важно понимать: качество данных — лишь половина успеха. Впереди остаётся не менее важный этап — анализ результатов и интерпретация эффекта, включая контроль ошибок I и II рода, выбор статистического метода и оценку мощности.

Продолжение — в Части 2: Анализ и интерпретация результатов A/B-тестов
Во второй части мы подробно рассмотрим, какие методы анализа применимы в условиях нестабильных офлайн-данных, как избежать ложных выводов и как адаптировать подход под конкретные метрики.

Книги и статьи:

• “Causal Inference in Statistics: A Primer”, Judea Pearl — отличное введение в причинные выводы.

• “Trustworthy Online Controlled Experiments”, Ron Kohavi — классика про AB-тесты, онлайн и офлайн.

• Avito.tech: «Как мы запускали новую модель продвижения»