
Хотелось быпоказать «суть» метода обратного распространения ошибки (Backpropagation) в нейросетях. Ведь ее сложно увидеть за нагромождением формул. Статья, конечно, не для профессионалов индустрии и математиков… Но знать производные нужно.
Рассматривать будем самый примитивный пример. С наименьшим количеством формул. А они, конечно, будут :-( Заранее прошу прощения за мои французские математические обозначения и термины. См. заголовок статьи (… на пальцах..).
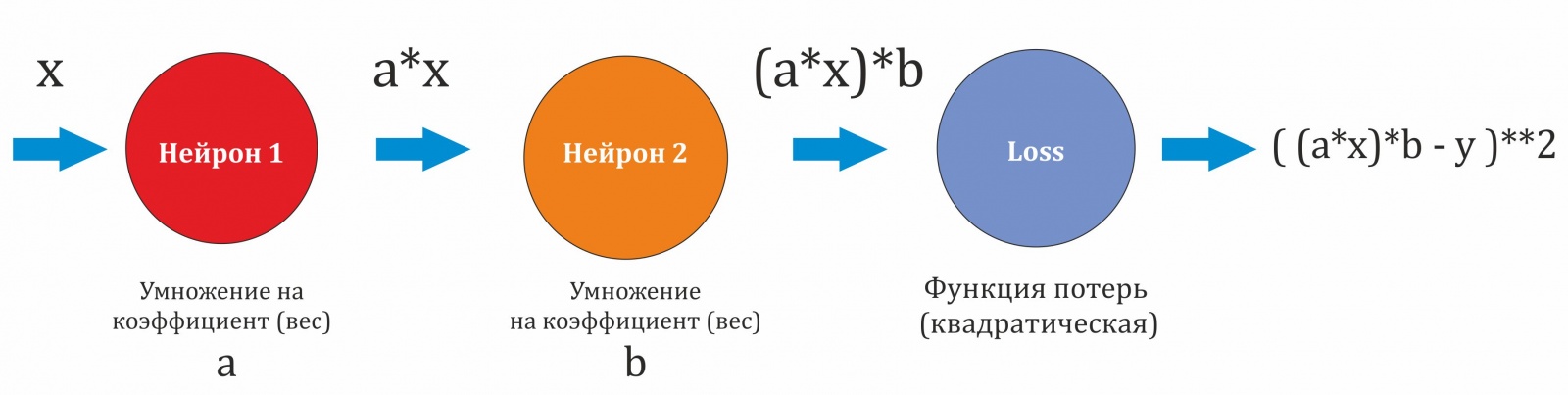
У нас только 2 нейрона, в каждом по одному коэффициенту (обозначим их a и b ). Нейроны последовательно передают свои результаты друг другу. В конце результат проходит через функцию потерь. Она квадратическая, имеет вид (х-y)**2 .
И, пока никакой функции активации у нейронов не будет. Ее мы добавим позже, принцип там тот же.
Ну вот теперь, к производным. Как вы можете знать, для подстройки коэффициентов (весов) нейросети, необходимо вычислить значение частной производной для конкретного коэффициента. Попробуем это сделать.
Возьмем частную производную по коэффициенту b , находящемуся в Нейроне 2.
https://www.wolframalpha.com/input?i=D[((ax%29b-y%29**2%2C%7Bb%2C1%7D%5D

Обратим внимание, что она состоит из 2х компонент. Это «цепное правило».
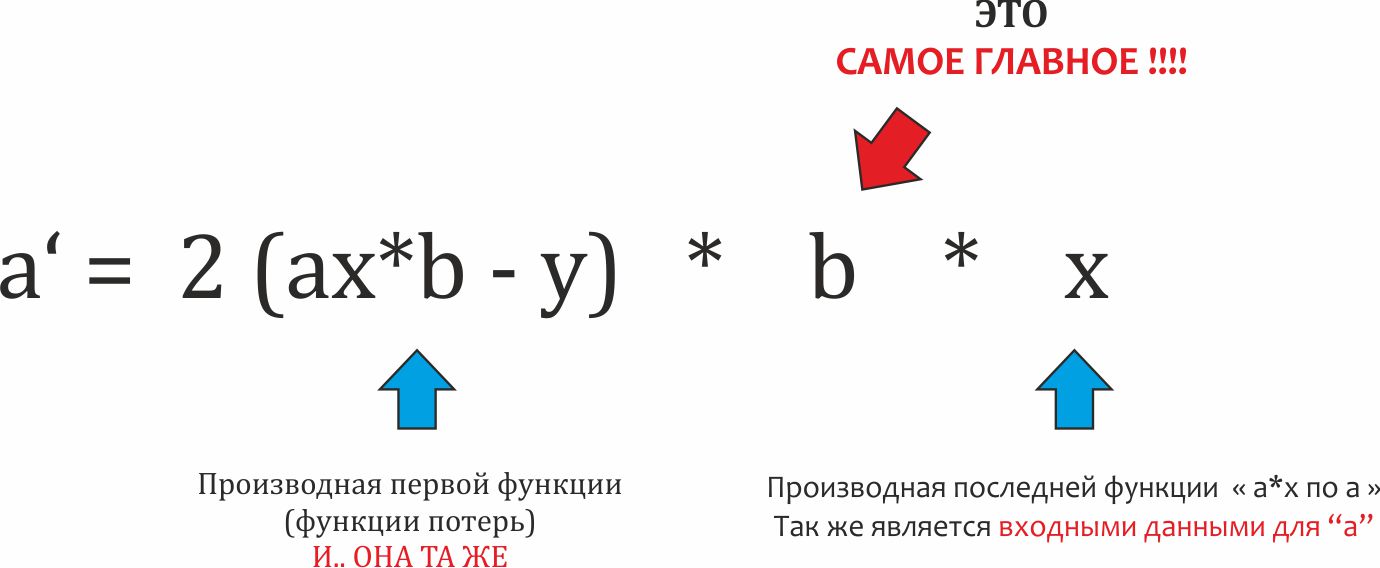
Не будем заострять внимание на нем самом, оно простое. Здесь важно заметить, что второй множитель это «входные данные». То есть, то что поступило на вход нашего множителя b.
Таким образом, производная для нашего коэффициента = значение производной «внешней» функции Х «входные данные» для данного коэффициента.
Прогнав данные через нашу «сеть» в прямом направление (forward) мы получим значения этих производных (ЧИСЛЕННО). То есть, они будут готовыми числами, и никаких формул писать не придется. Формулы нужны только сейчас Продолжим…
Теперь производная по коэффициенту а , находящемуся в Нейроне 1.
https://www.wolframalpha.com/input?i=D[((ax)b-y)**2%2C{a%2C1}]
Вот и ключ. Значение производной по внешней (для Нейрона 1) функции – это произведение всех предыдущих производных. Значение производной функции потерь у нас уже есть, а значение производной по Нейрону 2 – это просто коэффициент (b).
Итого
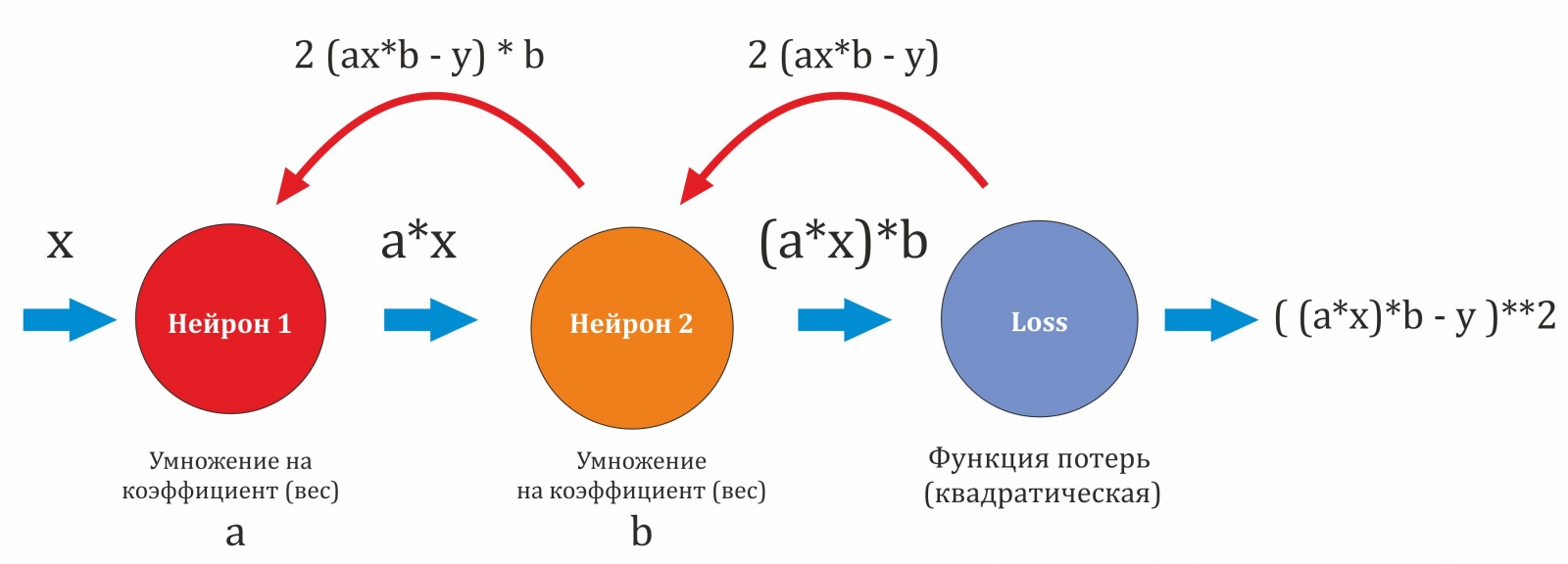
Теперь к коду на Python
# сами нейроны будут обьектами класса Neuron
class Neuron():
def __init__(self):
# У нейрона 1 коээфициет (вес). Установим его вот таким случайным числом.
self.ves = np.random.random()
# Те самые "входные данные". Будем хранить их в нейроне.
self.input = 0
# Поправки для весов
self.delta_ves = 0
# вычисление (прямой прогон)
def forward (self, x):
# сохранем те самые "ВХОДНЫЕ ДАННЫЕ". Они нам потребуются для обучения сети
self.input = x
# умножаем х на наш вес и возващаем
return x * self.ves
# с
def back (self, grad): # принимаем производную предыдущей функции
# производная для веса нашего нейрона = производная предыдущей функции * "входные данные"
self.delta_ves = grad * self.input
# производная для следующего нейрона = производная предыдущей функции * ТЕКУЩИЙ ВЕС ДАННОГО нейрона
# возвращаем их
return self.ves * grad
# применяем изменения к весу нейрона (ГРАДИЕНТНЫЙ СПУСК)
# Это можно делать ТОЛЬКО после передачи неизмененного (предыдущего) значения веса.
# здесь в виде отдельного метода
def fit (self, lr):
self.ves = self.ves - self.delta_ves * lr # производная * лернинг-рейn
# Модель будет просто списком из обьектов класса Neuron
class Model():
def __init__(self, num_neurons):
self.neurons = []
np.random.seed(5) # сид, для эксперементов
for i in range (num_neurons):
self.neurons.append( Neuron() )
m = Model(10) # пусть 10 нейронов
x = 5 # вход
y = 7 # ответ# это нужно крутить в цикле..
# прямой проход
for neuron in m.neurons:
ovtet = x
ovtet = neuron.forward(ovtet) # передаем данные с нейрона в нейрон
print(ovtet)
loss = (ovtet - y) **2 # вычисляем ЛОСЯ , квадратического
print("Лось = ", loss)
gradient = 2 * (ovtet - y) # берем производную последней функции (функции потерь)
lr = 0.01 # коэффициент шага для градиентного спуска
# ОБРАТНОЕ РАСПРОСТРОНЕНИЕ ОШИБКИ
for neuron in reversed(m.neurons): # двигаемся в обратном направлении (от последнего нейрона к первому)
# передаем значения производных
gradient = neuron.back(gradient)
# после передачи производной для следующего нейрона, применяем изменение к текущему нейрону
neuron.fit (lr)
Посмотрим на более сложную модельку.

Ситуация тут аналогичная. Каждый нейрон возвращает назад свой коэффициент.
Но может быть еще один вариант распространения данных по нейронам сети.

Теперь наш нейрон отдает результат в несколько нейронов на следующем слое. У нас полносвязная сеть. Теперь «возвратов» при обратном распространении несколько, а нейрон только один.
Попробуйте самостоятельно взять такую производную. Но ответ такой….. Их возвраты СКЛАДЫВАЮТСЯ.
Ознакомиться с полноценным кодом моего модуля для создания нейросетей вы можете здесь.
Там уже есть создание слоев с нейронами и добавление функции активации. Код, конечно, не учебный, с комментариями туго.
Спасибо.
Автор: falkorn


