Черный ящик с мозгами внутри: простое введение в нейросети

Введение

Сегодня мы поговорим о самых основах нейронных сетей, погрузимся в их первую архитектуру и постараемся понять, что скрывается внутри этой, на первый взгляд, волшебной коробки. Если ты новичок в машинном обучении – это статья для тебя.

Немного истории

Как многие знают, особенно те, кто родился до эпохи повсеместного распространения персональных компьютеров, изначально компьютеры создавались для математических вычислений и военных целей. В 1942 году был создан первый компьютер, отдалённо напоминающий наших современных “железных коней”.

Где-то в конце 1950-х годов был представлен первый прототип нейронной сети — персептрон. С тех пор идея нейросетей продолжала развиваться. Со временем учёные разработали фундаментальный алгоритм оптимизации — обратное распространение ошибки, а также различные функции активации, без которых невозможно представить современное машинное обучение.

Почему искусственный интеллект – искусственный

За вполне простым вопросом может скрываться ответ, который не только раскрывает сам вопрос, но и помогает лучше понять суть машинного обучения. Предлагаю немного порассуждать над этой темой.

Искусственный интеллект так и называют, потому что он представляет собой модель реального интеллекта. Конечно, в нашей голове не происходит сложных математических вычислений так, как это происходит в ИИ, но концепция нейросетей схожа с работой наших нейронов и связей между ними.

Искусственный интеллект обучается подобно ребёнку. Сначала малыш вообще не понимает, что происходит. Затем, в течение жизни, в его мозг поступает большое количество информации, на которой он учится. Родители объясняют: большие штуки с зелёной “шевелюрой” на улице — это деревья, а существо, которое бегает по комнате и издаёт звук “мяу”, — это кот.

Даже если ребёнок по ошибке подумает, что яблоко — это груша, другие люди его поправят: “Это не груша, это яблоко.” И если это повторять достаточно долго, ребёнок начнёт понимать свои ошибки и корректировать их.

Машины обучаются практически так же. Только вместо родителей — разработчики и учёные.

Архитектура первой нейронной сети: персептрон

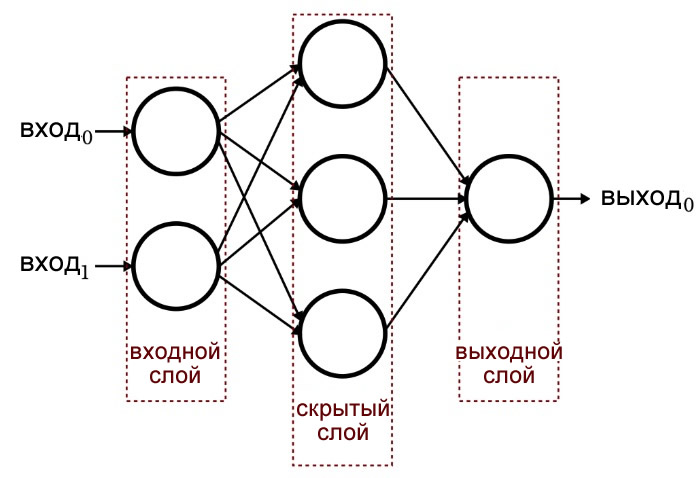
Знакомитесь – это персептрон и он настоящий дедушка среди нейронных сетей, но не смотря на свой возраст еще может быть эффективным, так что предлагаю разобрать его по частям.

Слои и нейроны

Начнём с самого простого — нейронов (их ещё называют узлами). Нейрон — это “кружок”, который вы видите на картинке. Именно в нём и происходят все вычисления, за исключением входных и выходных нейронов (но об этом — чуть позже в статье). Сейчас можно думать о нейроне как о месте, где совершаются основные вычисления.

Нейроны, расположенные вертикально друг под другом, образуют слой. Глобально таких слоёв всего три::

• Входной слой – это слой, куда поступают исходные данные. То есть именно сюда мы подаём входные значения. В типичной архитектуре персептрона во входном слое всегда одна колонка нейронов.

• Скрытый слой – это та часть сети, которая недоступна напрямую пользователю. Именно здесь происходят все ключевые вычисления (о них мы поговорим далее). В скрытом слое может быть любое количество нейронов, сгруппированных в один или несколько слоёв.

• Выходной слой – Это слой, где мы получаем результат после всех вычислений. Как и во входном, здесь обычно одна колонка нейронов.

Важно отметить, что входной слой мы называем ‘нулевым слоем’, так как у него нет ни весов, ни смещений. Грубо говоря, это просто место, куда мы складываем значения, и данный слой не вызывает большого интереса.

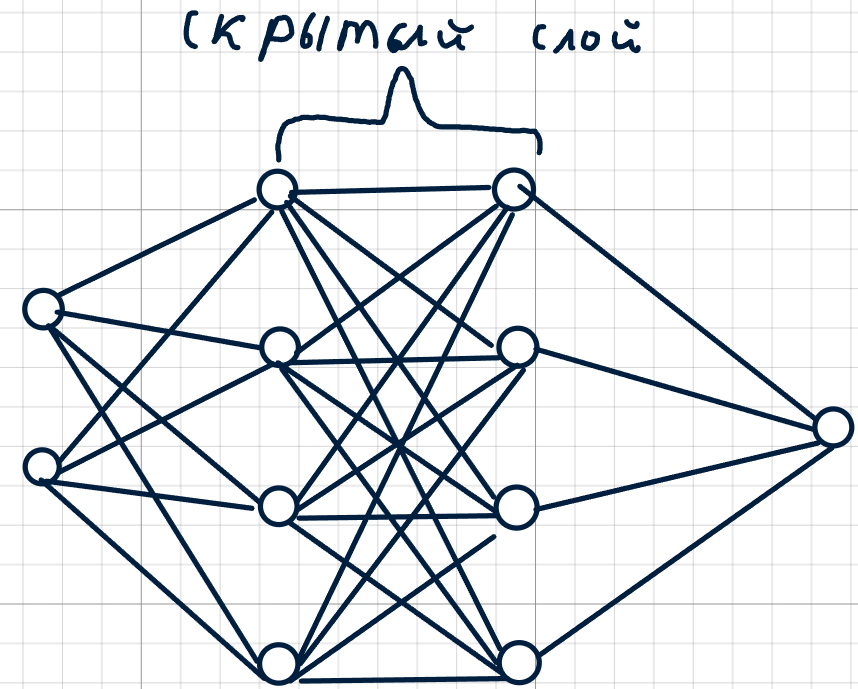
Сверху пример персептрона, у которого две колонки в скрытом слое.

Веса и смещения

Как я и говорил ранее, нейроны — это пока что для нас чёрная коробочка, в которой происходят вычисления. Чтобы понять, какое входное значение важнее, мы и вводим веса.

Фактически, вес(weight) — это просто число, на которое умножается входное значение. Так же веса обозначаются буковой w

Так как в процессе математических вычислений в нашей сети может возникнуть ситуация, когда на вход вообще не поступает сигнал (то есть значение равно нулю), возникает необходимость в использовании смещения. Оно позволяет всё равно генерировать выходной сигнал, даже при отсутствии входного. В противном случае нейрон просто “не сработает”.

Смещение (bias) — это тоже просто число, которое прибавляется к произведению входных данных на соответствующие веса. Смещения обозначаются буквой b

Отлично, мы разобрались с архитектурой персептрона, пришло время показать наглядно вычисления в нашей, пока что, сырой сети.

Как подбирать веса и смещения

Перед тем как приступить к вычислениям, хочу сразу ответить на данный вопрос: никак. Мы подбираем веса и смещения при оптимизации сети при помощи специальных алгоритмов. С самого начала мы случайным образом их инициализируем.

Вычисления в сети

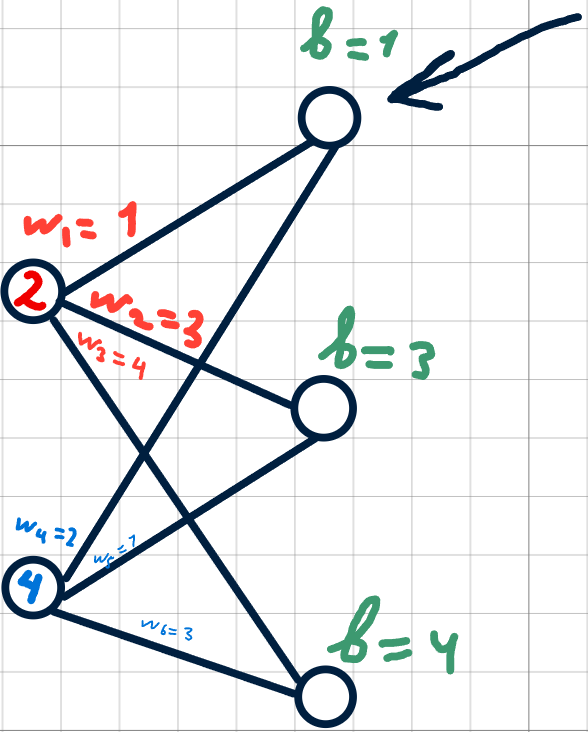
Так, у нас уже имеются веса и смещения, которые мы случайным образом инициализировали.

Предлагаю вычислить значение для 1 нейрона первого слоя.

Для этого нужно умножить значение первого нейрона нулевого слоя на соответствующий вес, далее получившийся результат сложить с произведением второго нейрона нулевого слоя на соответствующий вес и добавить соответствующее смещение. Согласен, звучит запутанно, проще показать это на практике:

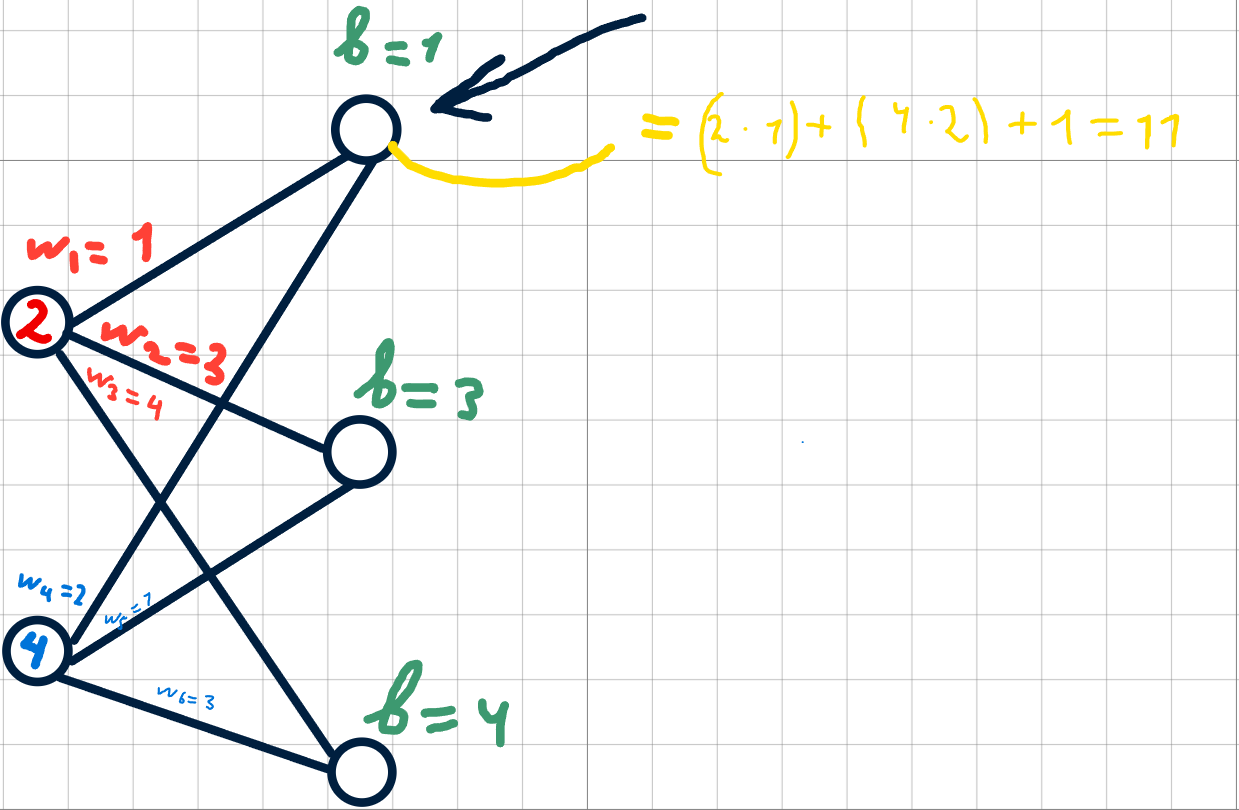
По такому же принципу и вычисляются другие нейроны в скрытом слое.

Погружаемся глубже. Вычисления в скрытом слое на уровне линейной алгебры

Согласитесь, что вычислять каждый нейрон вручную — это очень долго и муторно, так что давайте подключим линейную алгебру!

Мы можем представить входные значения в виде вектора x:

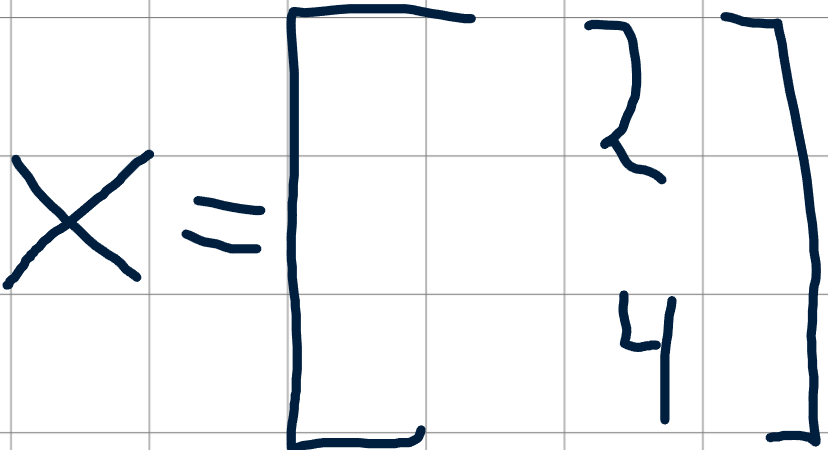
А значения весов в виде матрицы 2×3:

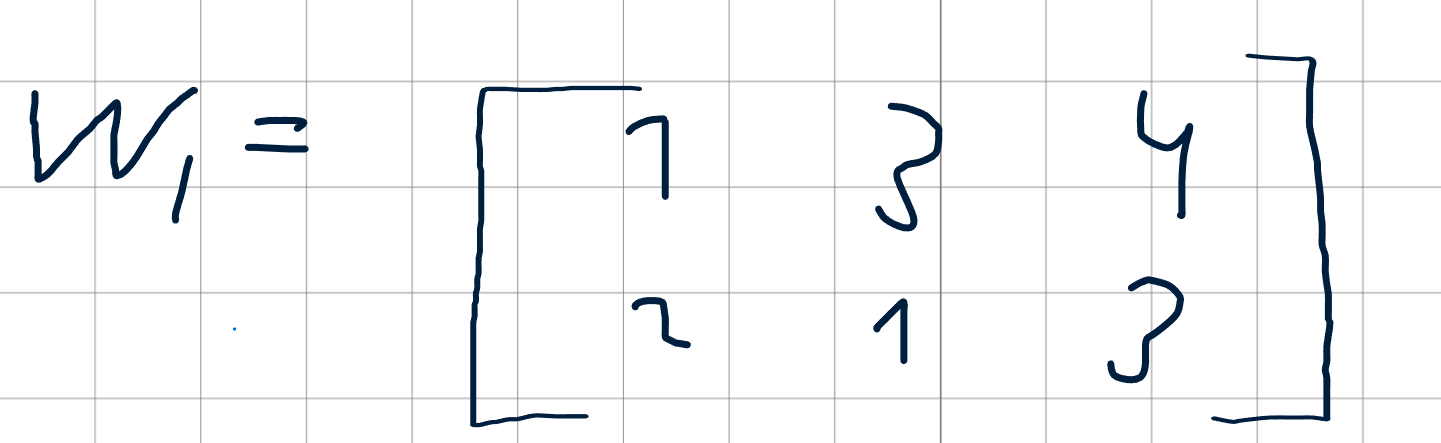
Индекс 1 означает, что это матрица для первого слоя.

Так же давайте обозначим вектор значений b:

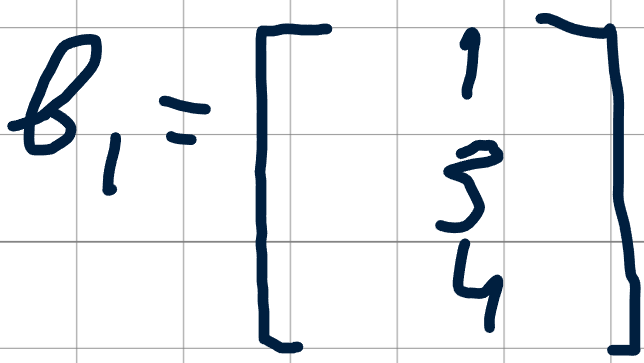
Отлично, теперь давайте просто умножим входной вектор на матрицу весов и сложим с вектором смещений:

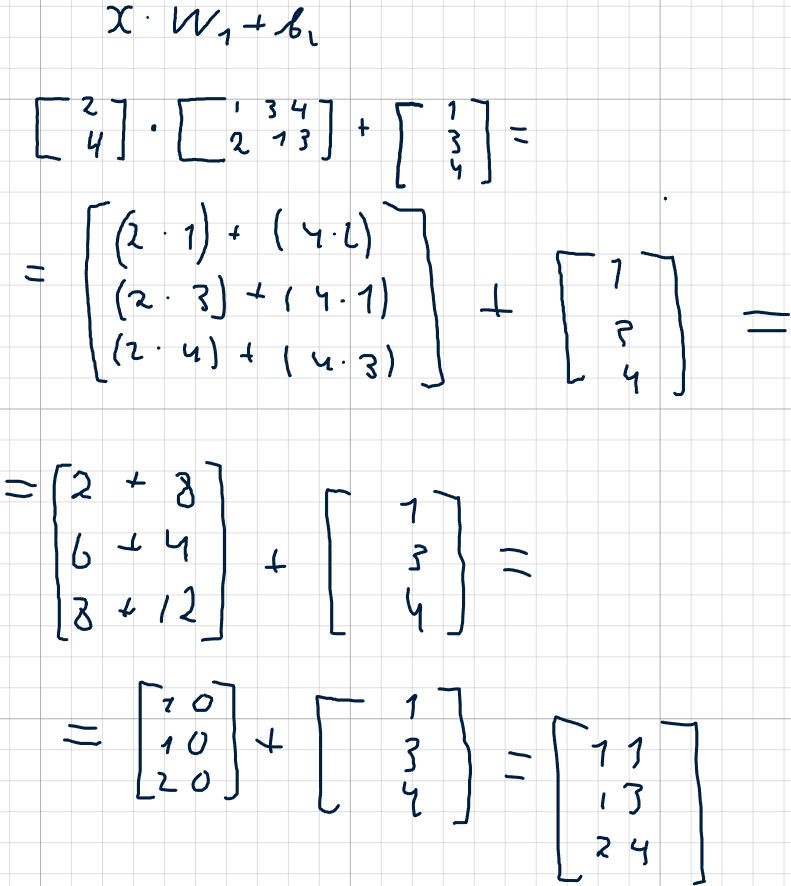
В итоге у нас получились те же значения, которые мы бы считали по очереди для каждого нейрона. На самом деле именно так выглядят первые вычисления в нейронах, но нас ждет еще кое что.

Функция активации

Перед нами стоит задача — преобразовать выходные значения нейрона в определённый диапазон, чтобы он мог гибко реагировать на различные ситуации.

Этот диапазон зависит от типа задачи, которую мы решаем.
Например, в бинарной классификации (то есть, когда нужно ответить “да” или “нет” — например, выдать ли человеку кредит), диапазон обычно задаётся от 0 до 1.

Число, полученное на выходе из функции активации, отражает степень “активности” нейрона — чем оно выше, тем сильнее нейрон “загорелся” и передаёт сигнал дальше.

Рассмотрим одну из самых простых и одновременно популярных функций активации — ReLU

Уравнение данной функции выглядит так:

Говоря простым языком, то:

• Если вход нейрона x <= 0, то функция возвращает 0.

• Если вход нейрона любое положительное число, то функция возвращает это же число.

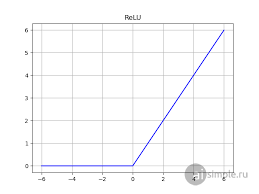
Важно, чтобы функция активации была нелинейной, иначе нейросеть превратится, по сути, в обычный калькулятор линейных преобразований.

Если бы в нейросети не было функции активации или она была бы линейной, то сеть могла бы решать только линейные задачи. А это сильно ограничивает её возможности, и нас, конечно, не устраивает.

На самом деле, выбор функций активации — очень ситуативен и зависит от конкретной задачи. Существует множество функций ошибок, каждая из которых лучше подходит для определённых типов задач.

Функция потерь

Пока что наша нейронная сеть, мягко говоря, сырая, и, конечно же, будет допускать ошибки. Чтобы оценить, насколько сильно она ошибается, мы вводим специальную функцию — функцию ошибки (или функцию потерь, loss function).

Функция ошибки возвращает числовое значение, и чем оно больше, тем хуже работает нейросеть.

В своём случае я буду использовать среднеквадратичную ошибку, или MSE (Mean Squared Error).

Формула данной функции:

где:

• n – количество примеров

• y_true – реальное значение

• y_pred – значение, которое нам сказала машина

Пожалуй, я наглядно покажу работу данной функции:

Шаг 1. Считаем разницу между истинными значениями и машинным предсказанием:

Шаг 2. Возводим ошибки в квадрат:

Шаг 3. Суммируем все квадраты ошибок:

Шаг 4. Делим на количество примеров:

Данный результат, в зависимости от задачи, можно интерпретировать по-разному.

Здесь и кроется одна из основных задач машинного обучения — оптимизация функции ошибки. Это достигается с помощью различных алгоритмов оптимизации, например, обратного распространения ошибки. Это уже отдельная тема для другой статьи, так что данный алгоритм мы рассмотрим позже.

Прямое распространение на python

Теперь мы готовы объединить все знания и реализовать это с помощью кода. Так как код будет достаточно длинным, а мы уже подробно разобрали все необходимые моменты, то я буду оставлять комментарии в коде только в случае острой необходимости.

Мы возьмем случайные данные и случайные значения.

import numpy as np

X = np.array([[0.1, 0.5]])  
y_true = np.array([[0.7]])  

w1 = np.array([[0.2, 0.4],  # Вес для нейрона 1 скрытого слоя
               [0.3, 0.1]]) # Вес для нейрона 2 скрытого слоя
b1 = np.array([0.1, 0.2])   # Смещение для скрытого слоя


w2 = np.array([0.5, -0.2])  # Вес для выходного нейрона
b2 = np.array([0.3])        # Смещение для выходного слоя


def relu(x):
    return np.maximum(0, x)
  
def mse_loss(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

# 1. Проходим через скрытый слой
z1 = np.dot(X, w1) + b1   
a1 = relu(z1)             

# 2. Проходим через выходной слой
z2 = np.dot(a1, w2) + b2  
y_pred = z2               

# 3. Вычисление ошибки (MSE)
loss = mse_loss(y_true, y_pred)

print("Предсказание:", y_pred)
print("Ошибка (MSE):", loss)

Что же такое прямое распространение? Это процесс, при котором мы “прогоняем” данные через нейронную сеть, начиная с входного слоя и заканчивая выходным.

Заключение

Мы прошлись от самых основ архитектуры персептрона и написали код на Python, который реализует прямое распространение. Надеюсь, мне удалось донести до новичков, что работа нейронной сети — это не волшебство, а результат применения математики.

Конечно, пока наша нейронная сеть ещё не идеально работает, и у нас есть куда расти. В следующих статьях мы будем обучать её и дорабатывать.