Propensity Score Matching (PSM): как обойтись без A-B-теста и всё равно узнать правду

На практике часто возникает необходимость объективно оценить, как то или иное событие влияет на ключевые метрики бизнеса. Это большая и широкая задача, которая часто решается с помощью проведения A/B-тестов. Но что делать, если провести честный рандомизированный эксперимент невозможно?

В таких ситуациях полезен метод Propensity Score Matching (PSM), который компенсирует отсутствие случайного распределения за счёт подбора сопоставимых групп для сравнения, снижает влияние скрытых факторов и обеспечивает более точную оценку причинно-следственного эффекта.

В статье я расскажу, что такое PSM, зачем и в каких случаях он необходим, опишу его теоретические основы, дам алгоритм его применения на практике и расскажу, как оценить качество и надежность полученных с его помощью результатов.

Что такое PSM?

Propensity Score Matching (PSM) — это статистический метод, который позволяет корректно сравнивать группы, уменьшая или полностью устраняя систематические различия между ними.

Предположим, у нас есть две группы пользователей: тестовая (treatment group), которая подвергается определённому воздействию (например, доступ к новой функции или участие в маркетинговой акции), и контрольная (control group), которая такого воздействия не получает. При этом между группами изначально есть систематическое смещение отбора (selection bias), выраженное в различиях ключевых характеристик пользователей (например, возраст, доход, активность). Наша задача — корректно оценить эффект воздействия, минимизировав влияние этих различий.

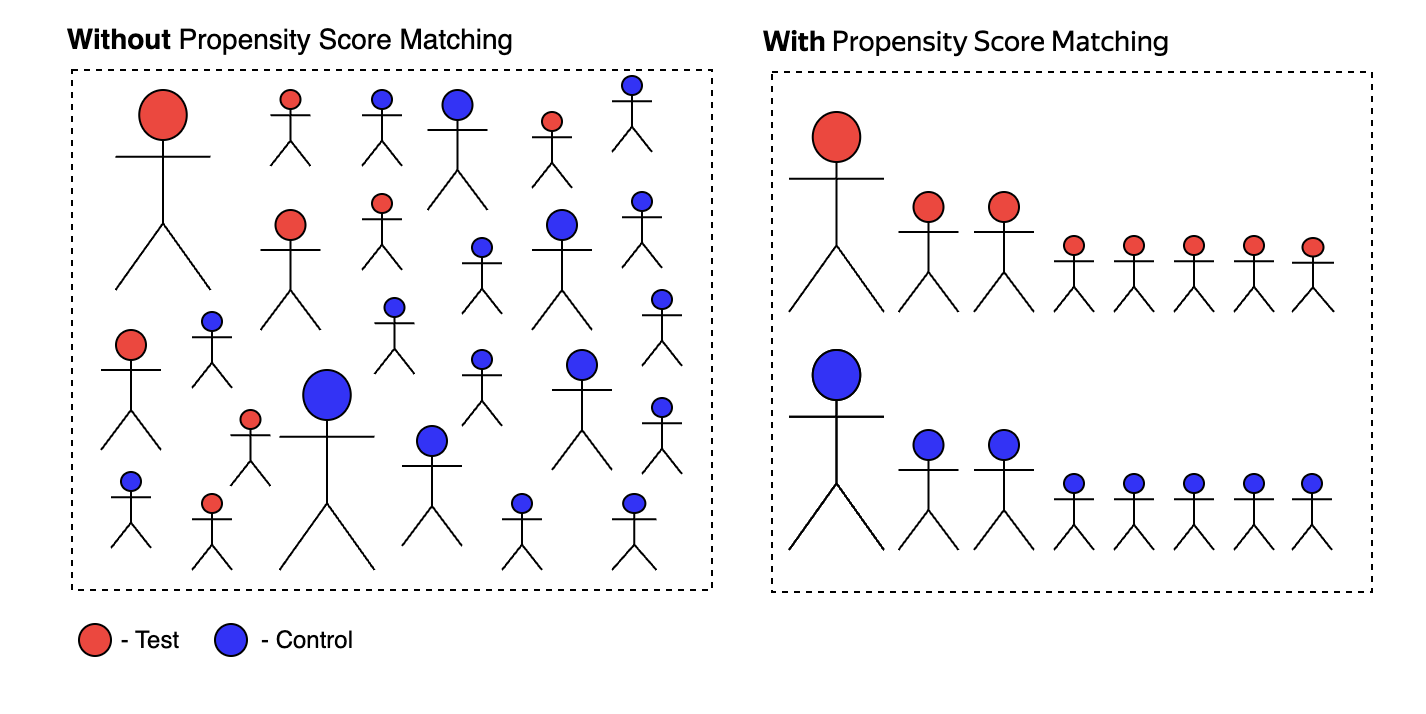
Основной принцип работы PSM заключается в том, чтобы для каждого пользователя из группы воздействия (treatment group) подобрать максимально похожего пользователя из контрольной группы (control group). Подбор осуществляется на основе ключевых характеристик этих пользователей, благодаря чему формируются пары, максимально схожие друг с другом. Это позволяет минимизировать исходные различия между группами и сделать корректный вывод о том, насколько именно воздействие повлияло на итоговый результат.

Зачем нужен PSM?

PSM полезен всегда, когда возникает систематическая погрешность отбора (selection bias), то есть когда результаты анализа искажаются из-за того, что группы для сравнения отличаются по характеристикам, существенно влияющим на изучаемый эффект.

Примеры таких ситуаций:

Невозможность или трудность проведения A/B-теста
Когда провести полноценный случайный эксперимент невозможно по техническим причинам, бизнес-ограничениям, этическим причинам или просто когда результаты нужны быстро и нет времени на организацию и проведение эксперимента.

Неслучайное формирование существующих групп
Когда группы сформировались естественным образом, и между ними уже имеются существенные различия, что затрудняет прямое сравнение.

Необходимость ретроспективной оценки эффекта
Когда нужно проанализировать исторические данные и понять, был ли эффект от уже реализованных изменений, хотя эксперимента не проводилось.

Повышение точности уже проведённых A/B-тестов
Когда даже в случайных тестах группы по каким-то причинам различаются по характеристикам, и необходимо снизить дисперсию оценок эффекта за счёт выравнивания групп по ключевым признакам.

Теория PSM

Тут будет немного формул, но я постараюсь сильно не усложнять и дать интерпретации ко всему что происходит.

Постановка задачи

Предположим, что у нас есть выборка:, где — вектор признаков объекта , — бинарная метка воздействия (treatment):

• , объект попал в treatment group (получил воздействие),

• , объект попал в control group (не получил воздействие).

Также предположим, что для каждого объекта существует два гипотетических результата (outcome) – значение метрики, которую мы хотим в эксперименте измерить:

• — результат, если бы объектполучил воздействие,

• — результат, если бы объектне получил воздействие.

Наша задача — оценить средний эффект воздействия на тех, кто получил treatment (Average Treatment Effect on the Treated, ATT):

Проще говоря, нам нужно оценить, как наше воздействие повлияло на тех, кто его получил.

Идея метода

Если факт попадания в treatment группу случаен и не зависит от признакового описания объекта, то есть:, то ATT можно оценить через разницу средних:

Проце говоря, если распределение на тест и контроль действительно случайно, то мы имеем дело с обычным рандомизированным экспериментом, и достаточно просто сравнить средние значения нашей метрики outcome в treatment и control группах – PSM не нужен.

Проблемы начинаются если назначение treatment не является случайным, а зависит от характеристик объекта , то есть . В таком случае прямое сравнение outcome между группами будет нерепрезентативным, так как разница в может быть обусловлена не только эффектом от воздействия, но и исходными различиями между группами.

Как же тогда оценить АTT? Формула состоит из двух составляющих:

Мы можем непосредственно оценить среднее значение результата для тех, кто получил treatment , так как для этих объектов наблюдается фактическое значение метрики после воздействия — то есть у нас есть реальные данные о том, как воздействие повлияло на их поведение или результат.

Однако величина (то есть результат для объектов, который был бы если тритмент группа не получила воздействия) остается неизвестной и требует оценки. Именно эту недостающую величину мы будем приближать с помощью Propensity Score Matching (PSM).

Как я уже говорил, идея метода состоит в том чтобы для для каждого объекта из контрольной группы подобрать максимально похожий объект из теста. Это делается для оценки.

Для этого в PSM необходимо:

Рассчитать propensity score — вероятность попадания объекта в treatment-группу на основе его признаков.

Подобрать похожие объекты (matching) — найти для каждого объекта из treatment-группы наиболее похожий объект из контрольной группы по propensity score.

Propensity score

Propensity Score (PS) — это вероятность попадания объекта в treatment-группу на основе его признаков:

По сути, расчет PS это классическая задача бинарной классификации с определением вероятности класса на выборке с таргетом .

Для её решения используются различные методы, в том числе:

• Логистичесая регрессия;

• Градиентный бустинг (XGBoost, LightGBM, CatBoost);

• Random Forest.

Для PSM ключевое требование к модели PS — хорошая калибровка вероятностей и учёт всех релевантных признаков.

По сути, алгоритм пытается “угадать”, кому назначили treatment, основываясь на их характеристиках. Если модель хорошо предсказывает, значит, в данных есть паттерн, по которому разделение на тест и контроль даётся не случайно. Если же вы уверены, что вы включили все необходимые признаки, но ответы модели близки к случайным, это может говорить о том, что в данном случае распределение между группами было случайным и вы можете просто сравнивать метрики по тесту и контролю.

Matching

После оценки propensity score, необходимо собрать из контрольной группы “псевдо-контрольную” группу, идентичную тритмент группе по распределению propensity score, чтобы с ее помощью оценить .

Задача Matching — подобрать для каждого объекта из тритемнт группы () такой (или такие) объекты из контрольной группы (), которые максимально похожи по значению propensity score.

Существуют различные подходы, некоторые из них:

• Nearest Neighbor Matching (NNM, k-ближайших соседей)
  Для каждого объекта из тритмент группы ищем ближайшего (или несколько ближайших) соседа(ей) из контрольной группы по метрике.

• Caliper Matching
  Модификация NNM, при которой разрешены только те пары, у которых разница в propensity score не превышает заданный порог : .

• Stratification Matching
  Ключевая идея: не искать “пары”, разбить выборку на бины по уровням (квантилям) propensity score, и сравнивать эффекты внутри этих групп.

Важно отметить, что при использовании NNM или Caliper Matching, не требуется чтобы в псевдо-контрольнной группе не было повторяющихся объектов. Условно говоря, может быть ситуация в которой один объект из контрольной группы сразу будет ближайшим соседом к нескольким объектам в тритмент группе.

В итоге, matching позволяет заменить ненаблюдаемые исходы для объектов из тритмент группы () на исходы наиболее похожих объектов из контрольной группы (), что позволяет оценить АTT:

Алгоритм исследования с помощью PSM

Определим treatment_date как дату, после которой объекты начинают подвергаться воздействию (Treatment, T).

Алгоритм состоит из следующих шагов:

Собрать исходный датасет с тестовой и контрольной группами. Размер тестовой группы – n, а контрольной группы – N >> n (например, 5n), чтобы обеспечить качественный подбор пар при метчинге. Проставить индикатор получения воздействия (T=1 — тест, T=0 — контроль).

Собрать релевантные признаки X для всех объектов датасета на данных за период до treatment_date.

Применить PSM: построить модель для расчёта Propensity Score и выполнить процедуру matching объектов. Получить из контрольной группы “псевдо-контрольную” группу.

Оценить качество метчинга – убедиться, что PSM работает (об этом немного позже).

Рассчитать целевые метрики (outcome) после treatment_date отдельно для тестовой и полученной псевдо-контрольной группы.

Замерить ATT.

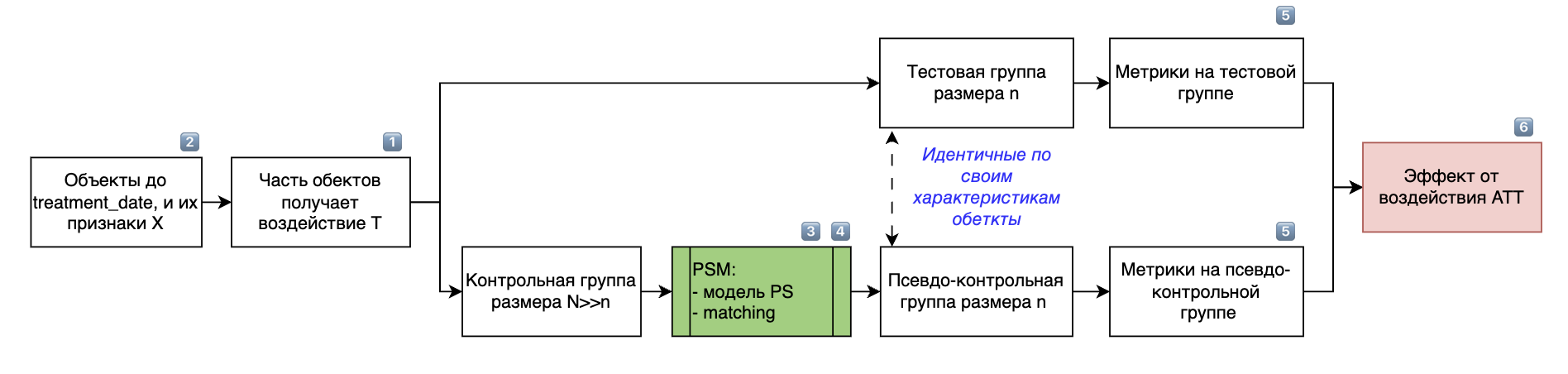
Как доказать, что PSM работает?

Вы провели исследование с использованием метода Propensity Score Matching. Как убедиться, что полученным результатам можно доверять? Для этого нужно доказать, что само распределение объектов на тестовую и псевдо-контрольную группы было выполнено корректно.

Следует обращать внимание на следующие моменты:

Отсутствие различий до воздействия (Pre-treatment validation)
Убедиться, что целевая метрика (outcome) в тестовой и псевдо-контрольной группах до даты воздействия (treatment_date) статистически не различается.

Качество модели Propensity Score
Модель Propensity Score должна корректно различать тестовую и контрольную группы: ROC_AUC (0.6+), и нет проблем с калибровкой. Модель не обязательно должна быть «лучшей» по точности классификации, но её прогнозы должны корректно отражать вероятность получения воздействия.

Статья про оценку качества прогноза вероятностей: Метрики оценки качества вероятностей в бинарной классификации: опыт из ФинТеха.

Баланс Propensity Score после метчинга
Распределения Propensity Score в тестовой и “псевдо-контрольной” группах должны быть статистически неразличимыми после выполнения метчинга.

Баланс признаков после метчинга (Covariate balance)
После выполнения метчинга распределения ключевых признаков в тестовой и псевдо-контрольной группах должны быть максимально схожими.

Соотношение размеров групп (Matching proportion)
Количество объектов в псевдо-контрольной группе после метчинга должно быть близко к размеру тестовой группы, без значительного дисбаланса в численности.

Проверка устойчивости результатов (Robustness Check)
Оценить, как изменится средний эффект воздействия (ATT) при изменениях в спецификации модели Propensity Score, методах метчинга или наборе используемых признаков. Эффект должен оставаться стабильным.

Общие рекомендации

Некоторые советы, которые могут быть полезны при проведении исследований:

• Контрольная группа должна быть больше теста
  Не забывайте, что в контрольную группу нужно набирать больше данных чем в тест (минимум тест должен быть в 5 раз больше контроля), это необходимо чтобы алгоритму метчинга было из чего выбирать пары для формирования “псевдо-контрольной” группы.

• Проводите сразу несколько вариантов исследования:
  Попробуйте использовать разные контрольные группы, наборы признаков, методы метчинга, принцип формирование контрольной группы, дату тритмента и тд.

• Не гонитесь за высоким ROC-AUC:
  Ваша цель не идеально различить тест и контроль, а корректно оценить вероятность попадания в тестовую группу (Propensity Score). Важно проверять калибровку модели.

• Внимательно собирайте признаки:
  Признаки должны быть рассчитаны исключительно по данным, собранным до начала воздействия, чтобы избежать утечки информации и смещения результатов.

• Помогайте модели на этапе формирования тестовой группы:
  При возможности заранее выбирайте тестовую группу, более близкую по характеристикам к потенциальному контролю — это облегчит дальнейший метчинг и улучшит точность оценки.

• Интерпретируйте полученные результаты:
  Старайтесь объяснять причины, почему именно тестовая группа показала лучшие (или худшие) результаты. Интерпретация повысит ценность и убедительность ваших выводов.

Надеюсь, эта статья была полезной и интересной для вас! Понимаю, что тема довольно объемная и ее можно раскрыть глубже. Если остались вопросы или хочется обсудить что-то подробнее — приходите в комментарии, буду рад помочь!

Другие статьи автора:

• Метрики оценки качества вероятностей в бинарной классификации: опыт из ФинТеха.

• Как банки предсказывают кредитные риски: опыт создания PD-моделей из ФинТеха.

• Машинное обучение и резервы банка: опыт из ФинТеха.