Всем привет! На связи команда аналитиков X5 Tech. Мы продолжаем исследовать подходы Reinforcement Learning для ценообразования. В этой статье мы рассмотрим применение контекстных многоруких бандитов на примере модельной задачи, опишем несколько реализаций и сравним их.
В предыдущих двух статьях мы разбирали вопрос применения Reinforcement Learning (RL) в виде многоруких бандитов (multi-armed bandits) для поиска оптимальных цен в задаче ценоообразования. В первой статье сравнили популярные стратегии многоруких бандитов для поиска оптимальной цены на один товар. Во второй показали, как можно учесть дополнительные условия, сведя задачу к оптимизационой с ограничениями.
В обоих случаях мы полагали, что магазины имеют одинаковый средний уровень спроса при единой фиксированной цене, а также считали, что спрос не меняется со временем. На практике магазины имеют разный уровень спроса, а также он может быть нестационарным, из-за чего использование простых многоруких бандитов усложняется, так как во всех подходах подразумевается, что мы должны брать отклик из одного и того же распределения, что вынуждает нас пробовать сгруппировать магазины так, чтобы средние продажи между группами были примерно равными, специальным образом обрабатывать сезонные факторы, тренды и т. д. Однако все эти ограничения естественным образом могут быть учтены в подходах, которые мы рассмотрим далее.
Сравнение методов RL
Приведём классификацию алгоритмов RL согласно книге:
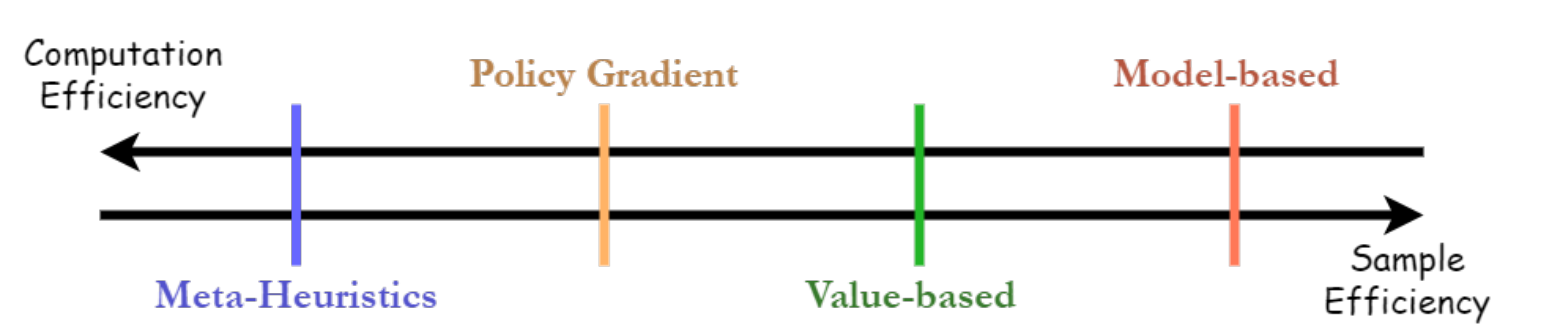
Meta-heuristic – подход рассматривает задачу максимизации метрики как задачу «black box оптимизации», то есть никаким образом не учитывает структуру взаимодействия между средой и агентом. Сюда можно отнести, например, генетические алгоритмы, имитации отжига и пр.
Policy gradient алгоритмы максимизируют метрику, используя оценки градиента функционала по параметрам стратегии (REINFORCE).
Value-based алгоритмы получают оптимальную стратегию неявно через теорию оценочных функций(Q-learning, DQN).
Model-based алгоритмы учат или используют предоставленную модель среды (MAB, контекстные MAB).
С точки зрения эффективности использования данных самыми неэффективными являются подходы, основанные на мета-эвристиках, а самыми эффективными, но при этом тяжеловесными, являются подходы model-based, что хорошо иллюстрирует картинка ниже:
Чтобы упростить сравнение разных видов RL, мы подготовили таблицу тех из них, которые в теории подходят для нашей задачи:
Таблица 1. Сравнение выбранных для задачи ценообразования моделей RL
|
|
MAB |
CMAB |
Q-learning |
DQN |
DDGP |
|
Тип задачи |
Выбор из конечного множества альтернатив |
Выбор действий с учётом контекста |
Обучение на дискретных состояниях и действиях |
Обучение на непрерывных состояниях и дискретных действиях |
Обучение на непрерывных состояниях и действиях |
|
Контекст |
Нет |
Есть |
Нет |
Есть |
Есть |
|
Пространство действий |
Дискретное, фиксированная сетка |
Дискретное, не фиксированная сетка |
Дискретное, фиксированная сетка |
Дискретное, фиксированная сетка |
Непрерывное |
|
Математическая основа |
Математическое ожидание награды |
Ожидаемая награда при условии контекста |
Q-значения и обновление наград |
Нейронная сеть для аппроксимации Q-функции |
Политики и функции ценности (Actor-Critic) |
|
Алгоритмы обучения |
ε-жадная стратегия, UCB, Thompson sampling |
ε-жадная стратегия, UCB, Thompson sampling |
Q-learning |
DQN, Double DQN, Dueling DQN |
Actor-Critic, TD3, Twin Delayed DDPG |
|
Скорость сходимости |
Быстрая |
Быстрая |
Медленная |
Медленное, требует много данных |
Зависит от сложности задачи |
|
Форма хранения |
Таблица с наградами для каждого действия |
Параметры регрессионной модели |
Таблица Q-значений |
Нейронная сеть для приближения Q-функции |
Две сети (Actor и Critic) |
|
Класс RL |
model-based |
model-based |
value-based |
value-based |
value-based + policy gradient |
Для нашей задачи поиска оптимальной цены в ценообразовании мы выбрали алгоритм CMAB по следующим причинам:
-
Это model-based подход, а значит позволяет учесть наши знания о задаче.
-
Нам важно минимизировать денежные потери во время исследования, с чем также хорошо справляется CMAB.
-
Ограниченное количество данных, что не даёт в полной мере использовать value-based и policy gradient подходы.
-
Хоть пространство действий и дискретное, модель позволяет предсказывать награды для любых цен, выбирая из них лучшую.
Подходы greedy, softmax, UCB, Thompson Sampling для MAB были изучены ранее, в том числе и в наших статьях, например, в этой. Рассмотрим применение подхода CMAB для ценообразования, сделаем обзор некоторых моделей и проведём численный эксперимент применения на синтетических данных.
Контекстные многорукие бандиты
Контекстные многорукие бандиты(CMAB) являются обобщением подхода многоруких бандитов. Цель остаётся прежней – выбрать оптимальную с точки зрения метрики ручку, но теперь ручка выбирается с учётом контекста – дополнительной информации об объекте, то есть на каждой итерации бандит видит признаковое описание объекта и исходя из этого оценивает отклик от разных ручек. Контекстный бандит занимается исследованием не только ручек, но и связи ручек с контекстом.
Применительно к ценообразованию ручками является набор цен, среди которых мы ищем наилучшую с точки зрения, например, маржи. Контекстом здесь может являться дата (сезон), магазин (например, его характеристики – площадь, ассортимент, близость к метро и т. п.), конкурентное окружение магазина (количество и состав конкурентов), погода. В нашем примере в качестве контекста мы будем использовать магазины и сезон в виде номера недели. Рассмотрим модель генерации данных для экспериментов.
Модель данных
Спрос в вычислительных экспериментах будем генерировать из пуассоновского процесса с интенсивностью событий :
где – время, отсчитываемое в неделях, начиная с нуля;
– номер магазина;
– установленная цена на товар;
В данном случае, кроме зависимости спроса от цены, мы хотим заложить в модель временную динамику и особенности каждого магазина. Исходя из этого была предложена следующая формула для расчёта интенсивности продаж:
где – интенсивность продаж магазина m при
=0 и
;
– сезонная составляющая или сезонный множитель;
– часть ответственная за зависимость спроса от цены;
– коэффициент, отвечающий за силу влияния сезонной составляющей на продажи;
– коэффициент, отвечающий за силу влияния отклонения цены от
на продажи;
– циклическая частота сезонной составляющей (рад./нед.);
– некоторая опорная цена, для которой выбирается интенсивность
, при
.
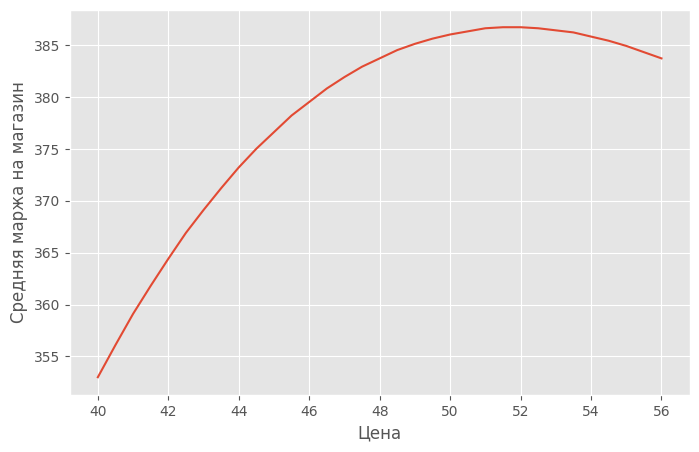
Пример сезонной составляющей, зависимости продаж и маржи
от цены представлены на рис. 1-3:

 = 48,
= 48,  = -1.5
= -1.5
 =
=  – годовая сезонность,
– годовая сезонность, 
 при
при 
Алгоритмы сэмплирования
Thompson Sampling(TS) и UCB
Для того, чтобы применять алгоритм TS, необходимо иметь возможность оценивать распределение потенциальных наград, что возможно выполнить благодаря байесовскому выводу – получению распределения параметров модели и, соответственно, распределения награды.
Для алгоритма TS нужно произвести сэмплирование параметров модели для каждого магазина и зафиксировать время
текущий номер недели, которые выступают в роли контекста. Далее произвести выбор той цены из сетки
, которая максимизирует наш показатель – маржу:
где – точечная оценка спроса в точке
при сэмплированом из апостериорного распределения параметров модели
.
Также байесовский вывод позволяет получить доверительный интервал для целевой функции, что можно использовать для подхода UCB (верхняя доверительная граница), в котором производится выбор ручки на оценках ожидаемой награды с учётом неопределённости этих оценок:
где и
– это оценка мат. ожидания спроса и стандартного отклонения в точке
, соответственно,
– параметр контроля уровня исследования.
Стратегии моделирования
Для контекстных многоруких бандитов необходима модель, с помощью которой будет оцениваться отклик для разных контекстов. Рассмотрим два варианта моделей – байесовская линейную регрессию и гауссовский процесс.
Байесовская линейная регрессия
Байесовская линейная регрессия(БЛР) предполагает, что между откликом и контекстом существует линейная связь. При этом, учитывая, что наши продажи распределены по Пуассону , мы можем описать обобщённую линейную связь через функцию экспоненты:
Цель байесовского вывода – получить апостериорные распределения оценок параметров на данных
и априорных распределений
:
здесь – в нашем случае пуассоновское правдоподобие.
Выпишем линейную относительно параметров модель, с помощью которой будем аппроксимировать данные для CMAB:
где – это смещение(константа);
– коэффициент, отвечающий за уровень продаж магазина под номером
, то есть здесь фактически провели one-hot-encoding, который необходим для описания различий в уровне продаж магазинов;
– коэффициенты, соответствующие разложению в ряд Фурье первого порядка для описания годовой сезонной компоненты с частотой
;
– параметры, отвечающие за зависимость от цены
– коэффициенты линейной комбинации log-log и log-lin моделей, которые часто встречаются в задачах поиска аппроксимации спроса от цены.
Сопоставляя с моделью генерации данных (1), можем записать связь между коэффициентами .
Получив апостериорное распределение параметров, мы можем воспользоваться одной из двух стратегией, применяемых для многоруких бандитов, а именно TS или UCB.
Схему применения данных подходов опишем ниже в “Схема эксперимента”.
Байесовский вывод для модели (4) будем производить с помощью библиотеки Python для вероятностного программирования PyMC. Эта библиотека позволяет численно производить байесовский вывод искомых параметров модели. В этой библиотеке формирование распределения осуществляется с помощью сэмплирования из апостериорного распределения через алгоритм Monte Carlo Markov Chain (MCMC) – конкретно его современной реализацией NUTS(No-U-Turn Sampler) – детальнее можно ознакомиться по ссылке.
Так как сэмплы параметров получаются из апостериорного распределения – их можно подставлять в модель для TS, а для вычисления доверительного интервала необходимо для каждого сэмпла рассчитать прогноз модели и получить статистики – среднее и стандартное отклонение:
.
Чтобы находить нелинейные зависимости между откликом и контекстом, можно использовать гауссовские процессы, некоторые варианты которых опишем дальше.
Гауссовские процессы
Гауссовские процессы (ГП) являются обобщением многомерного нормального распределения и используются для моделирования функций в задачах регрессии и оптимизации. В отличие от байесовской линейной регрессии, GP позволяет моделировать произвольные нелинейные зависимости, задавая их через ковариационную функцию (ядро).
GP предполагает, что любое конечное множество значений функции f(x) подчиняется многомерному нормальному распределению:
где — априорная средняя функция, обычно принимаемая равной 0 для упрощения;
— ковариационная матрица, элементы которой вычисляются с помощью функции ядра
.
Функция ядра определяет свойства функции: гладкость, периодичность и т. д. Например, ядро радиально-базисной функции (RBF):
где — масштаб вариаций, а
— длина масштаба (характерный размер корреляции).
Если отклики содержат шум
, это учитывается добавлением шума к ковариационной матрице:
Больше про выбор и создание ядер можно, например, узнать здесь.
Для предсказания на наборе точек рассчитывается апостериорное распределение значений функции
:
где
cреднее векторное предсказание: ,
ковариационная матрица: — ковариационная матрица для новых точек;
— ковариация между обучающими и новыми точками.
Для обновления параметров используется логарифм маргинального правдоподобия:
где Оптимизация проводится по гиперпараметрам ядра, например,
.
Для многоруких бандитов GP используется совместно с TS или UCB:
-
TS: Сэмплируется функция из апостериорного распределения
, и действие
выбирается как максимум этой функции.
-
UCB (Upper Confidence Bound): Для каждого действия вычисляется верхняя граница доверительного интервала:
,
где— среднее предсказание,
— стандартное отклонение, а
— параметр контроля исследования.
В нашем случае используется разреженная модель гауссовского процесса с пуассоновским правдоподобием (подробнее можно ознакомиться здесь, реализация подхода есть в библиотеке pyro), чтобы справиться с проблемой большого количества данных и учесть природу данных.
Кроме этого, в экспериментах используется глубокое обучение ядра для более гибкой аппроксимации данных. Этот подход подразумевает, что на вход модели подаются признаки, полученные из нейронной сети. Так как у нас имеется дифференцируемый лосс, эта сеть может обучаться вместе с ядрами стандартными градиентными методами.
Эксперимент и результаты
Схема экспериментов
Опишем основные шаги эксперимента:
-
Равномерное случайное распределение цен из сетки на все магазины.
-
Получение отклика в виде продаж спустя один период.
-
Обучение выбранной модели спроса на данных с учетом контекста.
-
-
Сэмплирование функции спроса для каждого магазина для алгоритма TS.
-
Оценка функции верхней границы доверительного интервала оценки показателя для каждого магазина для алгоритма UCB.
-
-
Выбор цен согласно формул (2) и (3) для алгоритмов TS и UCB соответственно.
-
Применение полученных цен к магазинам.
Далее повторяются шаги 1-6 несколько периодов, в нашем случае один период – неделя.
Цель – найти единую оптимальную цену на все магазины.
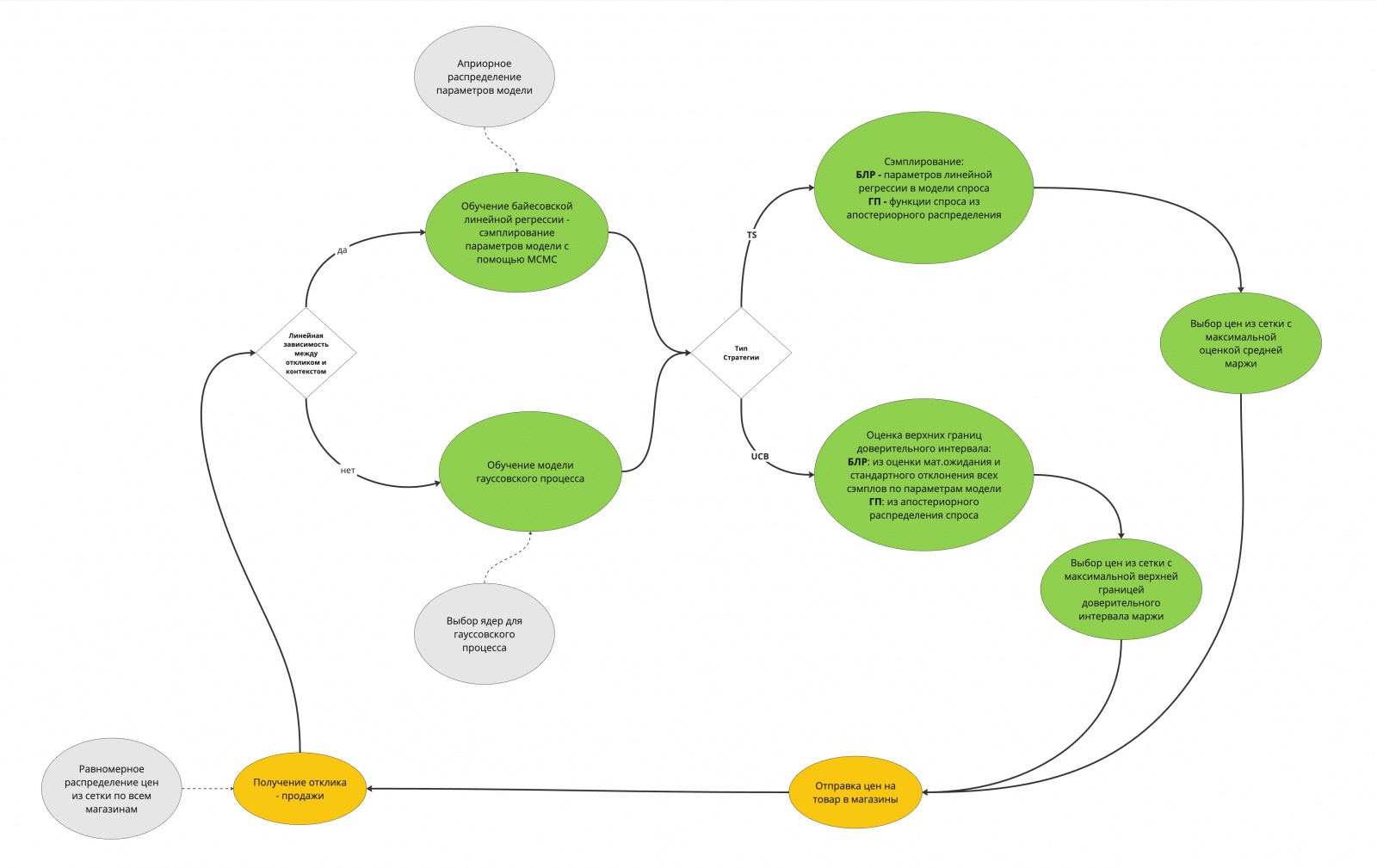
Все отличия в алгоритмах для TS и UCB в рассматриваемых моделях отобразили на схеме ниже:
Параметры модели генерации данных
Для эксперимента были выбраны следующие параметры:
Количество магазинов
Сетка цен
Параметры для генерации спроса (1) сэмплируются для каждого магазина и фиксируются в эксперименте из гамма распределения:
Это соответствует средним продажам 14.0 на магазин и стандартному отклонению 7.0,
Параметр = 33.0,
,
,
– количество периодов(недель)(включая нулевую с равномерным распределением цен по магазинам).
Количество повторений экспериментов для каждого алгоритма .
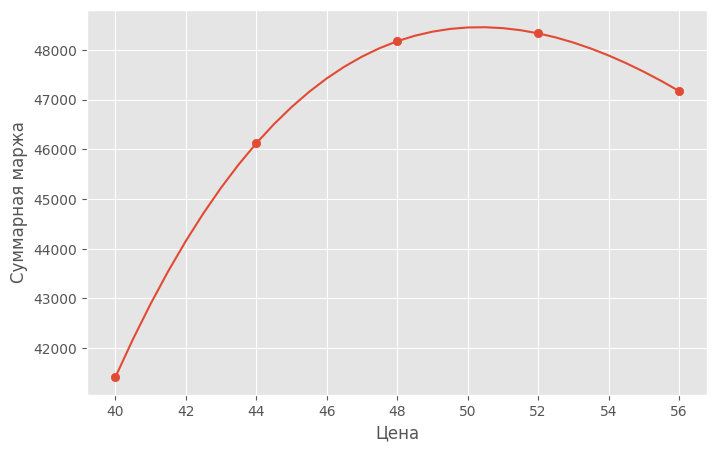
Суммарное матожидание целевой метрики для каждой цены из сетки
при
:
которе изображено в таблице 2. Там же указано, какую долю составляет маржа относительно оптимума в точке 52.0. Заметим также, что оптимум в точке 52.0 в рассматриваемой модели (1) не зависит от времени. График маржи от цены изображен на рисунке 5.
Таблица 2. Суммарное матожидание целевой метрики для рассматриваемых цен в эксперименте.
|
Цена |
Маржа |
Доля маржи от оптимума, % |
|
40 |
35891 |
86.3 |
|
44 |
39899 |
95.9 |
|
48 |
41582 |
99.9 |
|
52 |
41503 |
100.0 |
|
56 |
49468 |
97.3 |
Рассмотрим результаты моделирования для байесовской линейной регрессии и для гауссовского процесса.
Байесовская линейная регрессия
Для того, чтобы запустить расчёт, необходимо задать априорные распределения на параметры модели:
Результаты
В экспериментах были рассмотрены три стратегии: TS, UCB-1, UCB-2 (число после тире – значение в формуле (3)).
Эксперименты запускались, согласно схеме на рис. 4 для байесовской линейной регрессии. Количество итераций было установлено относительно небольшим в количестве 10 – это нужно было для того, чтобы провести весь ряд экспериментов за приемлемое время, на один прогон в 11 периодов в совокупности уходило 20-30 минут.
Рассмотрим результаты, которые получились в численных экспериментах.
Посмотрим на regret и накопленный regret в процентах от оптимума, которые изображены на рис. 6. Regret здесь считался следующим образом: на каждой неделе определялось матожидание маржи при оптимальной цене, далее из этого значения вычиталось матожидание маржи при установленной цене:
regret % считается как процент regret от оптимального значения в каждый момент времени t:

Как мы видим, в данном случае алгоритмы UCB-1 и UCB-2 обгоняют TS, между UCB-1 и UCB-2 практически не наблюдается различий.

По динамике цен на рис. 7 видно, что все алгоритмы к шагу 1 практически не выбирают самую худшую цену на сетке 40.0, которая отличается от оптимума на 13.7%(таблица 2), к шагу 2 она полностью исключена как бесперспективная. К шагу 2 все модели исключают вторую худшую цену 44.0. То, что модели практически сразу исключают цену 40.0, связано тем, что уже на 0 шаге получается адекватно описать ценовую зависимость. На рисунке 8 изображена гистограмма сэмплов параметров и
(взятых из априорного и апостериорного распределений), отвечающих за ценовую зависимость на одном из экспериментов. Как мы видим, распределение этих параметров сдвигается к истинным значениям(рис. 8).
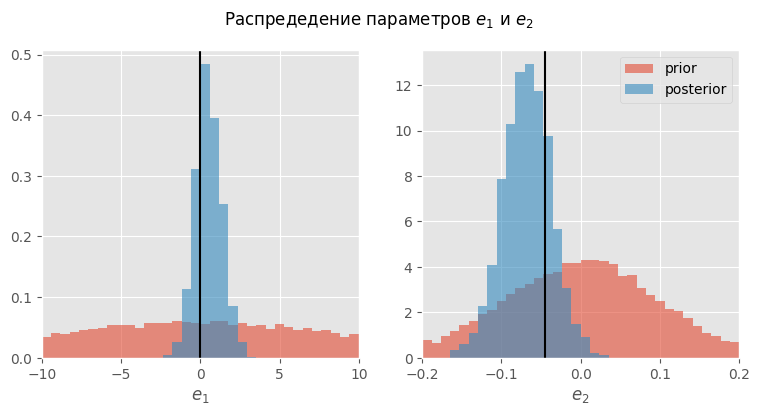
Оценка зависимости средней маржи от цены в таком случае изображена на рисунке 9. Здесь градиентом серого от тёмного к светлому указаны интервалы в 1, 2, 3 стандартных отклонения. Видно, что цена 40 с учетом доверительного интервала хуже тех, которые больше 44.0.
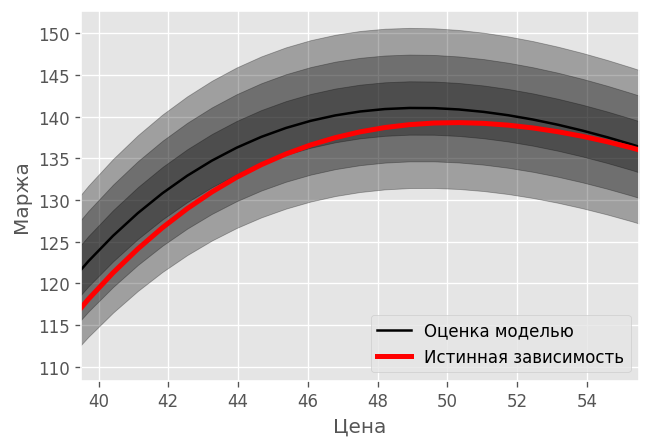
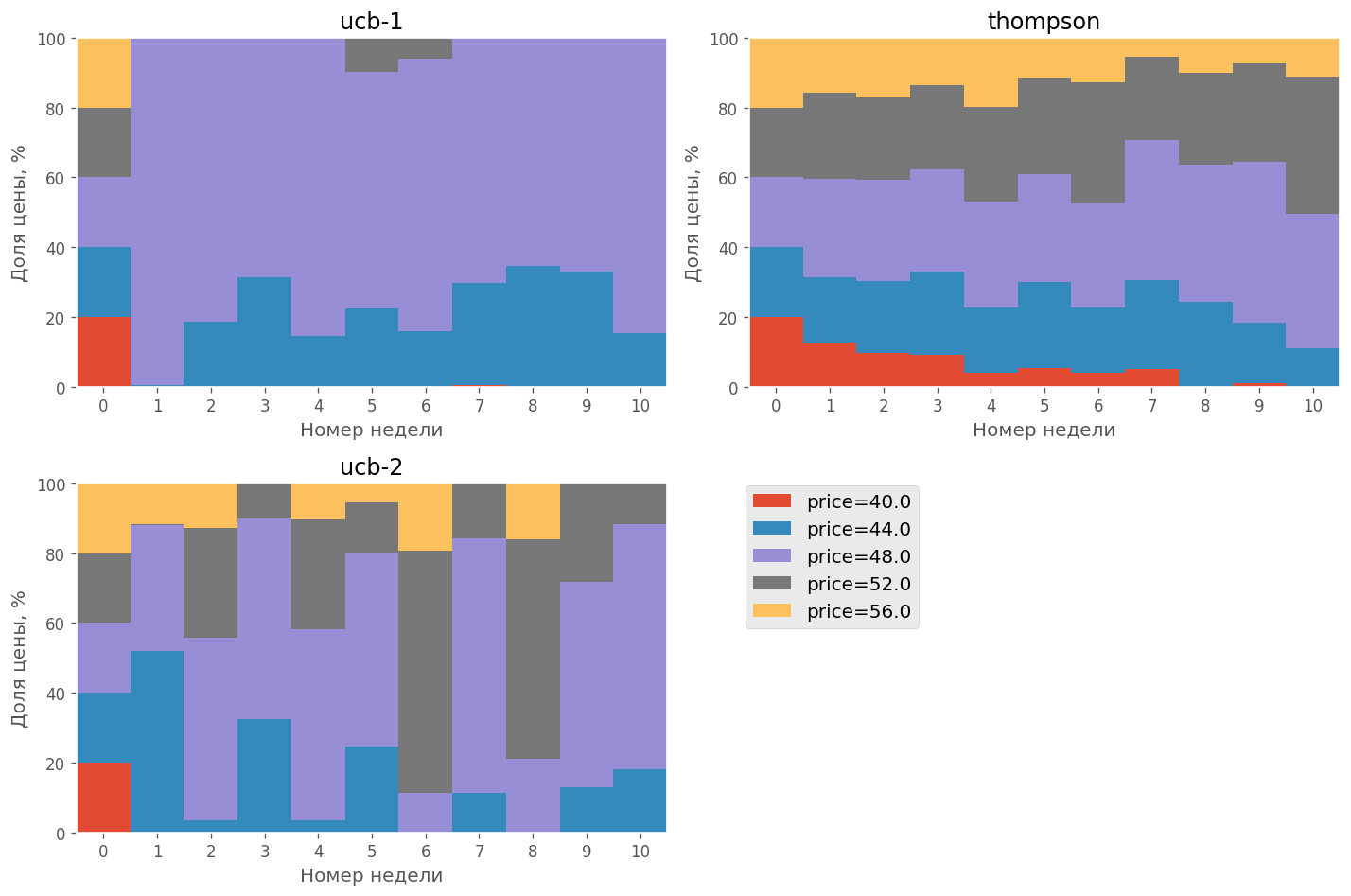
После второго шага алгоритмы выбирают варианты преимущественно среди двух цен 48.0 и 52.0, к десятому шагу чаще выбирается оптимальная цена 52.0 (таблица 3).
Таблица 3. Средние доли цен в % на последнем периоде эксперимента
|
|
Цена |
||||
|
Алгоритм |
40 |
44 |
48 |
52 |
56 |
|
TS |
0.0 |
0.0 |
36.1 |
63.3 |
0.6 |
|
UCB-1 |
0.0 |
0.0 |
40.1 |
60.0 |
0.0 |
|
UCB-2 |
0.0 |
0.0 |
39.9 |
60.1 |
0.0 |
Такое поведение связано с тем, что маржа в этих точках отличается на 0.1%, и алгоритмы статистически не могут различить эти две точки из-за такого малого различия, но в целом, если судить по динамике TS, то выглядит так, что по мере набора статистики чаще выбирается оптимальная цена по мере накопления данных. Как мы видим, в такой ситуации есть ненулевая вероятность выбора субоптимальной цены.
Если пользоваться критерием – выбираем самую часто встречающуюся цену за последние 3 недели, то алгоритмы UCB выбирают между ценам 48.0 и 52.0 приблизительно 50/50%, а TS выбирает оптимум в 90% случаев.
Гауссовский процесс
Эксперимент с гауссовскими процессами запускался аналогично предыдущему по схеме из рисунка 4. Здесь для большей гибкости мы использовали подход с глубоким обучением ядра, то есть вместе с остальными параметрами на входе ядра обучается нейронная сеть
. Один прогон в 11 недель занимал около 3-4 минут. Далее приведён рисунок 10 с динамикой regret % и cumulative regret % и таблица 4 с показателями для сравнения по результатам экспериментов с учётом байесовской линейной регрессией:
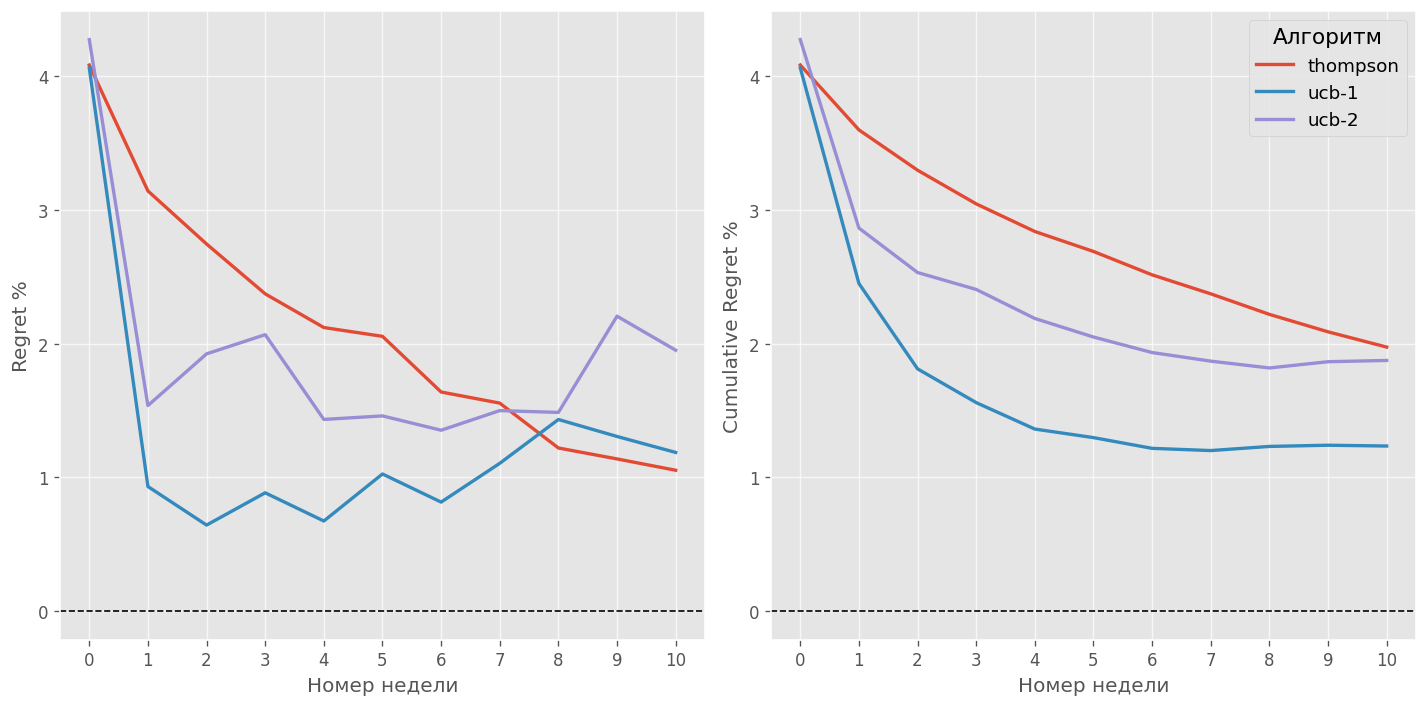
Таблица 4. Суммарные показатели по неделям 0-10 включительно для линейной модели и гауссовского процесса
|
Модель |
Алгоритм |
Regret % |
|
Байесовская линейная регрессия |
TS |
0.66 |
|
Байесовская линейная регрессия |
UCB-1 |
0.56 |
|
Байесовская линейная регрессия |
UCB-2 |
0.55 |
|
Гауссовский процесс |
TS |
2.0 |
|
Гауссовский процесс |
UCB-1 |
1.4 |
|
Гауссовский процесс |
UCB-2 |
1.6 |
По таблице видно, что в экспериментах с гауссовским процессом подход UCB в среднем показал себя лучше. Однако стоит отметить, что подход UCB на графиках показывает нестабильное поведение, что также можно увидеть на рис. 11 – доля цен для UCB сильно скачет, тогда как TS, хоть и медленно, но стабильно сходится, чаще выбирая оптимальную и субоптимальную цену. Можно предположить, что медленная скорость сходимости TS обусловлена недостаточным обучением модели гауссовского процесса.
Заключение
Мы провели сравнение моделей RL для задачи ценообразования, по результатам которого был выбран метод контекстных мнгоруких бандитов. Далее детально изучили алгоритмы UCB и TS для линейного и нелинейного вариантов зависимости отклика от контекста. Перечислим основные выводы, которые мы получили в результате моделирования.
Для алгоритма на базе байесовской линейной регрессии:
-
Алгоритм сходится к оптимальному решению.
-
UCB показал лучшие, по сравнению с TS, результаты по показателю regret.
-
UCB проигрывает TS, если критерий выбора лучшей ручки – наиболее часто выбираемая алгоритмом цена.
-
При выборе модели и алгоритма важно ориентироваться на тот критерий и показатель, который преследует эксперимент.
Для гауссовского процесса:
-
UCB по метрикам также показал себя лучше, но TS показал себя более стабильным.
-
Несмотря на то, что метрики для гауссовского процесса оказались хуже, чем для байесовской линейной регрессии, данный подход имеет запас для улучшения путём подбора лучшего ядра и более тщательного обучения.
Общий вывод – подход с контекстными многорукими бандитами показал сходимость для модельной задачи с учётом контекста магазинов и наличия сезонного фактора в продажах.
Над статьёй работали Михаил Будылин, Егор Горюнов и Антон Денисов.
Автор: muxeu


![Контекстные бандиты в ценообразовании - 52 lambda(p, m, t)=exp{w_0 + sum_{i=1}^{n} w_i I[i=m] + \ a_1 cdot sin(omega_0 cdot t) + a_2 cdot cos(omega_0 cdot t) + \ e_1 cdot ln(p) + e_2 cdot p} tag{4},](https://www.braintools.ru/images/2025/01/06/kontekstnye-bandity-v-cenoobrazovanii-52.svg)



