Изобретаем polimer — фреймворк на Python для ускорения разработки научных прототипов

Еще с третьей версии в Python появились аннотации типов, которые можно использовать в качестве комментариев к аргументам функций, для статического анализа и поиска ошибок или даже перегрузки методов в зависимости от типов аргументов. Помимо данных применений авторы Python оставили разработчикам возможность реализации своих сценариев. В этом туториале мы разработаем мини-фреймворк для автоматического построения цепочки вызовов, что позволит уменьшить объем интерфейсной части кода и упростить его масштабирование на дальнейших этапах.

Введение

Для начала напомним зачем нужны аннотации. Наиболее популярный вариант применения – это аннотация типов, которая позволяет обозначить типы передаваемых аргументов и возвращаемых значений, а за одно выявлять ошибки в коде:

# Все нормально (результат функции - строка)
def greeting(name: str) -> str:
    return 'Hello, ' + name

# Ошибка (некорректный тип результата - число, а ожидается строка)
def greeting(name: str) -> str:
    return 123

Менее известный вариант применения – это перегрузка операторов на основе передаваемых аргументов. В примере ниже вызывается либо первая, либо вторая функция в зависимости от типа аргумента name.

from multimethod import multimethod

@multimethod
def greeting(name: str) -> str:
    return 'Hello, ' + name

@multimethod
def greeting(name: list) -> str:
    return 'Hello, ' + ', '.join(name)

Кроме того, аннотации можно использовать для указания человеко-читаемых комментариев к аргументам без какой-либо синтаксической нагрузки для интерпретатора:

def greeting(name: 'Имя пользователя') -> str:
    return 'Hello, ' + name

Существует множество других вариантов, но мы сразу перейдем к нашему подходу.

Основной подход

В нашем туториале мы предлагаем использовать аннотации не просто как идентификатор типа аргумента (напр. число или строка), а в качестве идентификатора полезной нагрузки (напр. цена акции или название компании). Таким образом можно неявным образом связать между собой функции и классы, выполняющие логически связанную последовательность действий (например, выгрузка исторических котировок, преобразование, вычисление рисковых показателей и визуализация конечного результата), а с помощью фреймворка объединить эти действия в одну команду.

В дальнейшем с развитием кода реализация внутренних методов может изменяться и даже появляться новые, но фреймворк позволит автоматически перестраивать цепочки вызовов, опираясь на заданные нами аннотации. Таким образом, разработчик может сконцентрироваться на разработке логики прототипа и отложить решение некоторых архитектурных вопросов на более поздние итерации.

Образ результата

Прежде чем приступить к реализации давайте рассмотрим описанный выше подход на тривиальном примере вычисления средней цены акций за некоторый промежуток времени:

prices.py

import random

def get_prices(length=10) -> 'price_list':
    return [random.random() for _ in range(length)]

def calc_avg_price(p: 'price_list'):
    return sum(p) / len(p)

main.py (без фреймворка)

from prices import *
price_list = get_prices(10)
avg_price = calc_avg_price(price_list)

Обратите внимание, что идентификатор ‘price_list’ входного аргумента функции calc_avg_price() совпадает с идентификатором результата функции get_prices(), что позволяет объединить оба метода в один, например так:

main.py (с фреймворком)

from prices import *
from polimer import prices
avg_price = prices.calc_avg_price()

В данном примере отсутствует вызов функции get_prices(), т.к. он происходит автоматически, а результат подается на вход функции calc_avg_price(). Аналогичным образом можно упростить и более сложные цепочки вызовов, но для начала давайте реализуем описанный подход.

Реализация

Давайте перечислим что необходимо сделать для реализации описанной выше идеи на практике:

• Выгрузить список всех доступных методов и их аннотаций – список методов находится в служебном реестре sys.modules, а их аннотации из __annotations__

• Составить дерево/граф зависимостей – для этого будем использовать графовую структуру в виде списка смежностей, где узлами являются функции, а ребрами их зависимости по аргументам (например, когда результат работы одной функции является аргументом для другой, то между ними устанавливается ребро на графе)

• Провести топологическую сортировку узлов графа – чтобы вызов каждого последующего метода происходил строго после того, как были проинициализированы все требуемые аргументы

• Реализовать мета-функцию, которая будет строить и вызывать цепочки получившихся зависимостей исходя из того, какой конечный метод необходимо запустить (prices.calc_avg_price() в примере выше)

• Пробросить мета-функцию в составе публичного модуля (from polimer import prices в примере выше)

А теперь давайте детально рассмотрим реализацию каждого из описанных выше шагов. Начнем с выгрузки списка методов и аннотаций:

import sys, inspect

def load_functions():
    functions = {}
    for module_name in sys.modules:
        for item in vars(sys.modules[module_name]).values():
            if (inspect.isfunction(item) == True) and (len(item.__annotations__) > 0):
                f_id = item.__module__ + "." + item.__name__
                functions[f_id] = item
    return functions

Далее, составляем дерево зависимостей:

def build_dep_tree(functions):
    f_ids = {} # artifact_id -> function_id map
    dep_tree = {}
    for f_id in functions:
        artifact_id = functions[f_id].__annotations__.get("return", None)
        if artifact_id != None: f_ids[artifact_id] = f_id
    for f_id in functions:
        dep_tree[f_id] = []
        annotations = functions[f_id].__annotations__
        for argument in annotations:
            dep_artifact_id = annotations[argument]
            dep_f_id = f_ids.get(dep_artifact_id, None)
            if (argument != "return") and (dep_f_id != None):
                dep_tree[f_id].append(dep_f_id)
    return dep_tree

Для удобства понимания давайте представим дерево зависимостей на примере тривиального фрагмента кода:

import random

def get_range() -> 'num_days':
    return 30

def get_prices(l: 'num_days') -> 'price_list':
    return [random.random() for _ in range(l)]

def calc_avg(p: 'price_list', l: 'num_days') -> 'average_price':
    return sum(p) / l

Для такого фрагмента дерево зависимостей будет выглядеть следующим образом:

Дерево зависимостей

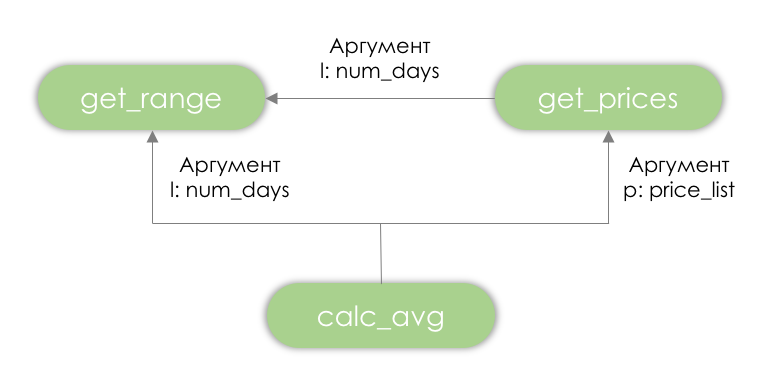
Допустим, мы хотим вызвать функцию calc_avg() – как сформировать цепочку вызовов, в которой все зависимые функции расположены после функций, от которых они зависят? Для этого достаточно произвести топологическую сортировку:

from collections import deque

def topology_sort(dep_tree, start_f_id):
    res_deque = deque()
    visited = set()
    stack = [[start_f_id]]
    while stack:
        for f_id in stack[-1]:
            if (f_id in visited) and (f_id not in res_deque):
                res_deque.appendleft(f_id)
            if f_id not in visited:
                visited.add(f_id)
                stack.append(dep_tree[f_id])
                break
        else:
            stack.pop()
    result = list(res_deque)
    result.reverse()
    return result

Дерево зависимостей (после топологической сортировки)

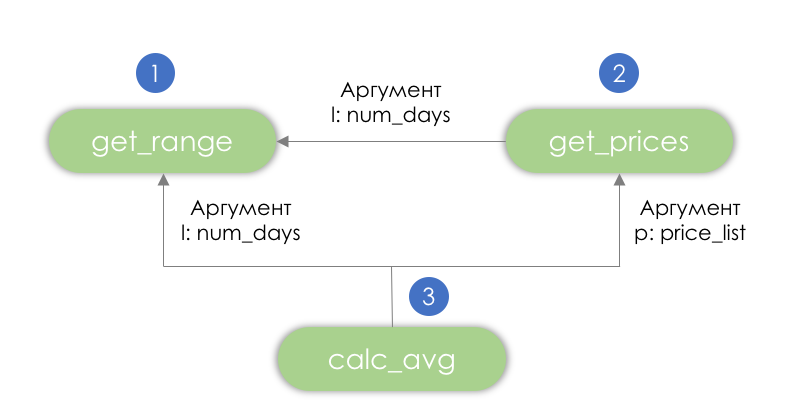
Как мы видим, первой следует вызывать функцию get_range(), после нее get_prices(), а затем calc_avg().

Далее нужно написать мета-функцию, которая будет строить цепочку вызовов исходя из заданной точки входа и последовательно вызывать эту цепочку, сохраняя промежуточные результаты на каждом шаге.

def run_chain(chain, functions):
    result = None
    artifacts = {}
    for f_id in chain:
        res = functions[f_id]()
        artifact_id = functions[f_id].__annotations__.get("return", None)
        if artifact_id != None: artifacts[artifact_id] = res
        result = res
    return result

def run(f_id):
    functions = load_functions()
    dep_tree = build_dep_tree(functions)
    chain = topology_sort(dep_tree, f_id)
    return run_chain(chain, functions)

Мета-функция run() производит описанные выше шаги – инициализирует список доступных методов, строит дерево зависимостей, осуществляет топологическую сортировку и вызывает сформированную цепочку. Для вызова цепочки реализован отдельный метод run_chain(), внутри него заводится словарь artifacts, хранящий промежуточные результаты.

Теперь нам необходимо пробросить интерфейс мета-функций наружу для удобства пользователя. Для этого заведем виртуальные подмодули (с помощью типа ModuleType) в реестре globals(), куда и пропишем мета-функции. Напомним, что виртуальные подмодули нужны, чтобы исключить возможные коллизии в названиях методов:

from types import ModuleType
from copy import deepcopy

def get_func(f_id):
    def func(**kwargs):
        return run(f_id, kwargs)
    return func

functions = load_functions()
__all__ = []

for f_id in functions:
    module_name, function_name = f_id.split(".", 1)
    if module_name not in globals():
        globals()[module_name] = ModuleType(module_name)
        __all__.append(module_name)
    setattr(globals()[module_name], function_name, deepcopy(get_func(f_id)))

__all__ = tuple(__all__)

Наконец, осталось объединить код нашего мини-фреймворка воедино, сформировать дистрибутив и загрузить его в репозитарий PyPI, чтобы его можно было устанавливать через pip install. Эти подробности мы не будем описывать, но вы можете посмотреть готовый результат в конце статьи. Теперь любой метод можно импортировать из нашего фреймворка следующим образом:

prices.py

def get_range():
   #...

def calc_avg():
   #...

main.py

from prices import *
from polimer import prices

prices.calc_avg()

Как видите, мы сократили цепочку вызовов с двух до одного метода (т.е. в 2 раза). Уже неплохо, но давайте посмотрим что будет, если применить фреймворк в более реалистичной задаче из области финтеха. Финтех был выбран исключительно для наглядности и в будущем мы можем с одинаковым успехом рассмотреть любую другую область, например телекоммуникации, искусственный интеллект или даже квантовые вычисления.

Прикладной пример (финтех)

Для наглядности мы рассмотрим одну из актуальных задач в области финтеха – определение рыночного режима (от англ. market regime detection) на основе наблюдений исторических биржевых котировок. Понимание текущего рыночного режима позволяет инвесторам условно разделять временные интервалы на периоды стабильности и кризисов, высокой и низкой волатильности, высокого и низкого уровня риска, а также принимать решения на основе такой классификации.

На иллюстрации ниже вы можете увидеть один из вариантов классификации состояний экономики за периоды с 1971 года по 2021-ый год. Примечательным является то, что периоды финансового кризиса 2008-го, а также ковидного 2019-го годов отмечены фиолетовым цветом. В нашем примере мы также будем рассчитывать, что кризисные периоды будут отмечены отдельным классом, что подтвердит корректность работы алгоритма в связке с фреймворком polimer.

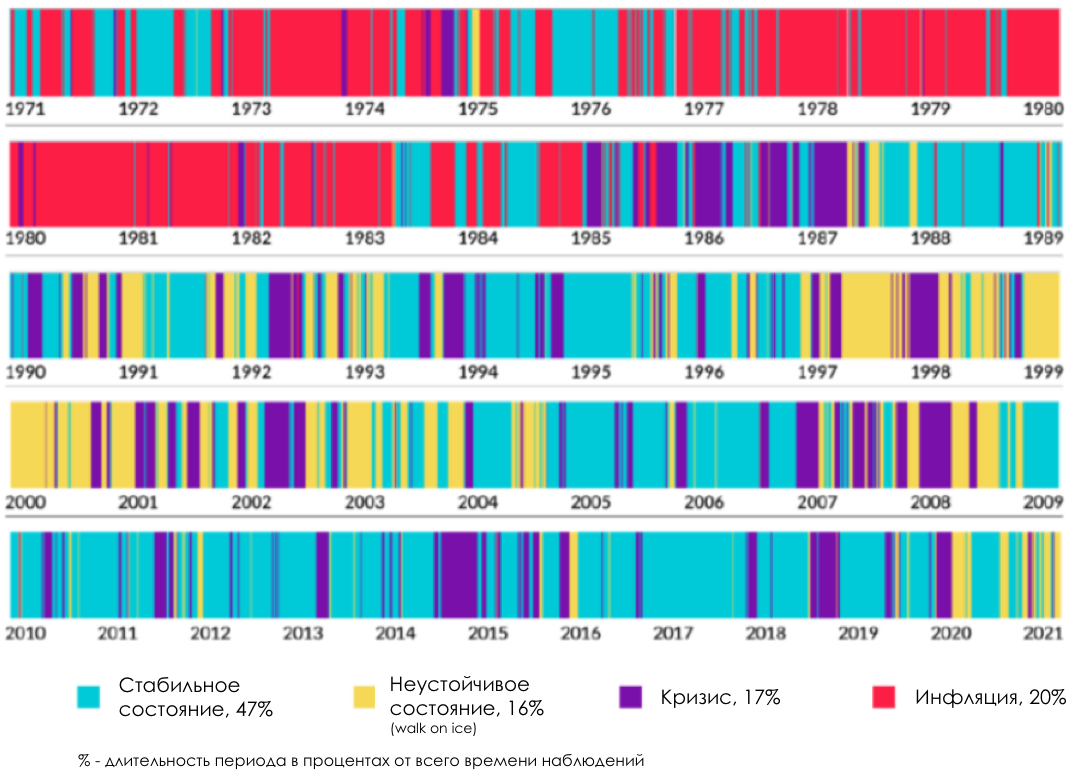
С точки зрения машинного обучения эта задача относится к классу методов обучения без учителя (unsupervised learning) и может решаться с помощью таких подходов как скрытые гауссовские Марковские модели, модели гауссовых смесей или даже обычным k-means подходом. Чтобы не сильно отходить от нашей основной темы мы не будем вдаваться в детали каждого подхода, а возьмем готовую реализацию метода скрытой гауссовской Марковской модели из библиотеки hmmlearn.

А теперь давайте рассмотрим поэтапно, как осуществить классификацию рыночных режимов на основе исторических биржевых котировок, а также как можно упростить эту задачу помощью фреймворка polimer.

• Во-первых, необходимо выгрузить сами биржевые котировки за исторический период. Мы возьмем их из открытых источников с помощью утилиты yfinance (yahoo finance). В качестве данных будем использовать котировки траста SPDR S&P 500 ETF (старое название Standard & Poor’s Depositary Receipts), которые торгуются на бирже NYSE Arca под кодом SPY (тикер)

• Далее, нам понадобится предобработать данные сырых котировок, чтобы посчитать два производных показателя – доходность и диапазон цены за сутки

• Следующим шагом мы обучим модель на основе скрытого гауссовского марковского процесса, а также проведем классификацию на базе обученной модели

• В заключении, проведем визуализацию полученного результата в виде графика с цветовой индикацией определенных нами рыночных режимов

Мы не будем подробно описывать каждый этап, а приведем код всех описанных выше шагов сразу. Обратите внимание на аннотации методов (через двоеточие), с первого взгляда они не несут существенной нагрузки, но чуть позже вы поймете насколько сильно это упростит наше взаимодействие с кодом, благодаря polimer-у.

pip install polimer yfinance hmmlearn pandas numpy matplotlib

market_regimes.py

import numpy as np
import pandas as pd
import yfinance as yf
from hmmlearn import hmm

def load_data(index="SPY") -> "data":
    data = yf.download(index)
    return data

def prepare_dataset(data: "data") -> "dataset":
    returns = np.log(data.Close / data.Close.shift(1))
    range = (data.High - data.Low)
    features = pd.concat([returns, range], axis=1).dropna()
    features.columns = ["returns", "range"]
    return features

def train_model(dataset: "dataset") -> "model":
    model = hmm.GaussianHMM(
        n_components=3,
        covariance_type="full",
        n_iter=1000,
    )
    model.fit(dataset)
    return model

def predict_states(data: "data", dataset: "dataset", model: "model") -> "states":
    states = pd.Series(model.predict(dataset), index=data.index[1:])
    states.name = "state"
    return states

def plot_regimes(data: "data", states: "states"):
    color_map = {
        0.0: "green",
        1.0: "orange",
        2.0: "red"
    }
    pd.concat([data["Close"], states], axis=1).dropna().set_index("state", append=True)["SPY"].
        unstack("state").plot(color=color_map, figsize=[16, 12])

А теперь давайте посмотрим как можно получить конечный результат – график с рыночными режимами. Для наглядности приведем 2 листинга – один с помощью фреймворка polimer и второй без него.

from market_regimes import *
data = load_data(index="SPY")
dataset = prepare_dataset(data)
model = train_model(dataset)
states = predict_states(data, dataset, model)
plot_regimes(data, states)

from market_regimes import *
from polimer import market_regimes

market_regimes.plot_regimes(index = "SPY")

Как видите, код с полимером стал более лаконичным, а все основные шаги (выгрузка и предобработка данных, обучение модели и классификация) выполняются автоматически. Аналогичный эффект можно достичь не только при классификации рыночных режимов в финтехе, но и для любой другой задачи, в которой вычисления осуществляются в несколько этапов по типу конвейера.

Давайте запустим получившийся код и рассмотрим внимательно полученный результат. На графике ниже представлены исторические котировки индекса SPY с выделенными разными цветами рыночными состояниями, которые были классифицированы нашим алгоритмом. Примечательно, что кризисные периоды 2008 и 2019-х годов отмечены отдельным цветом, что в целом соответствует ожиданиям и подтверждает корректность работы алгоритма в составе фреймворка.

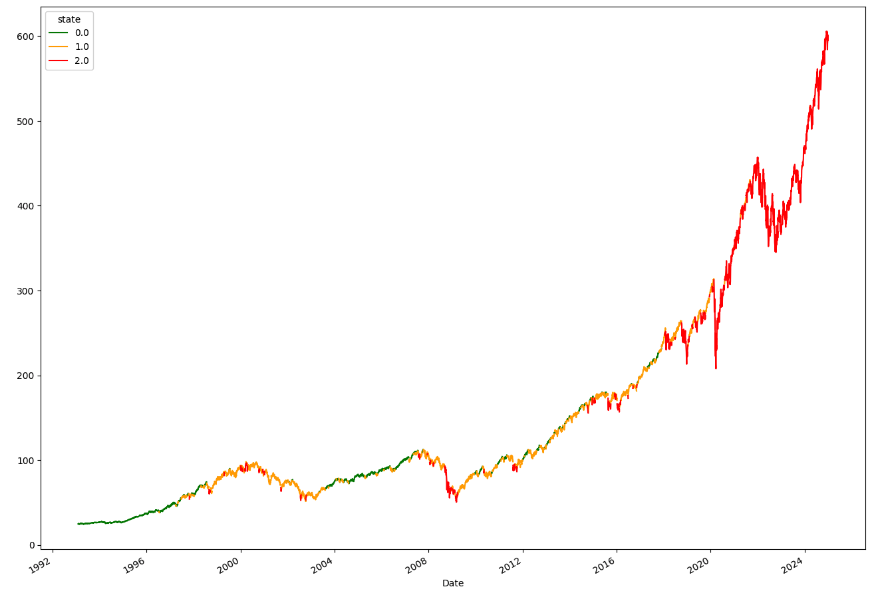
На этом наш туториал подошел к концу, а в заключение хотелось бы отметить, что успех прикладной ИТ-разработки все чаще зависит не только от качества решения целевой задачи, но и от своевременного развития структурного инструментария, упрощающего масштабирование стартового прототипа в промышленный продукт. А если вы занимаетесь экспериментальной разработкой и хотите подготовиться к успешному выводу своего ИТ-продукта на рынок в будущем, не стесняйтесь обращаться к нам в комментариях или личных сообщениях – мы с удовольствием рассмотрим ваш кейс и поможем спроектировать оптимальный ИТ-инструментарий.

Всех с наступающими праздниками и ярких открытий в Новом году!

Ссылки на материалы из статьи:

• Исходный код фреймворка

• Определение рыночных режимов

• Упаковка PyPI репозитариев