Небольшой бенчмарк (вроде этого): генерируем данные, потом тренируем на них нейросеть (DL – deep learning) и статистические модели (ML – machine learning). Оценивать результат будем по точности (Confusion Matrix) и контурному графику Decision Boundary, а также по времени тренировки. Мы классифицируем синтетические данные тремя способами (на разном количестве данных, от 1000 до 100 000 примеров):
-
DL модель с одним слоем из 8 нейронов
-
Support Vector Classifier
-
Decision Tree Classifier
В статье даются основные настройки DL модели. Затем – выводы и результаты приводятся в конце для справки, чтобы не загромождать полезное место. Те же самые результаты можно получить запуская код из Google Colab. Код в статье приводится не весь, а только необходимый. Детали – в блокноте.
Decision Boundary и TensorFlow Playground
Архитектура нейросети в данной статье рассматривается одна. С целью изучения архитектур нейросети, можно также посмотреть TensorFlow Playground. В нем можно визуально редактировать нейросеть и смотреть на результат, делая обучение шаг за шагом, наблюдая значения коэффициентов. Там своя нейросетевая библиотека, не TensorFlow (и нет классического ML). Зато есть возможность покопаться в исходниках. Обратите внимание на столбец Output на рисунке ниже. Там дана Test Loss и как раз показана Decision Boundary. Мы будем такую же картинку получать и использовать в качестве визуальной характеристики.
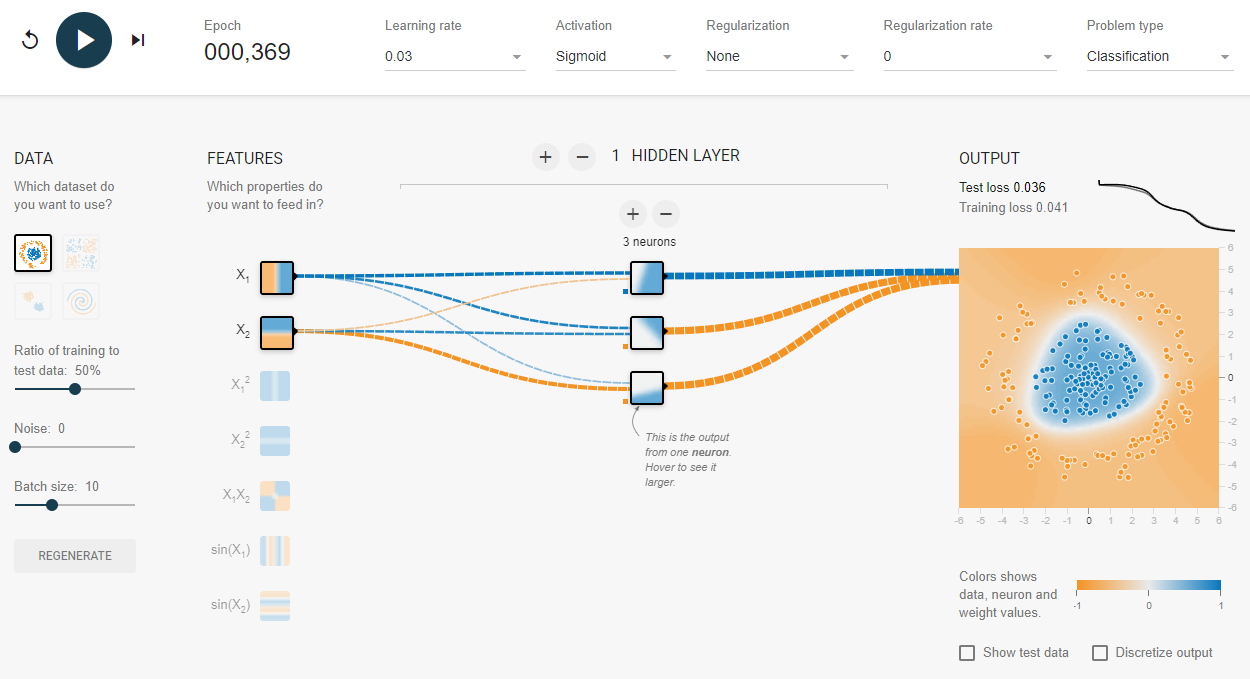
Сепарабельность данных и количество нейронов
Сепарабельные данные должны иметь расстояние между классами, чтобы данные классифицировались тремя нейронами. На рисунке выше видно что между группами оранжевых и синих точек есть кольцевой зазор. В моем случае, зазора нет (рисунок будет ниже) и нужно минимум – 6 нейронов (см. код в Google Colab по ссылке ниже). Это требование к количеству нейронов возникает из-за того что классы прилегают плотно друг-к-другу и “зазор” между голубыми и оранжевыми метками в моем наборе небольшой (его почти нет). Если, в секции генерации данных, сделать вместо:
blue_points_separable = blue_points[distance_from_origin_blue > 1.0]что-то такое:
blue_points_separable = blue_points[distance_from_origin_blue > 1.4]То можно будет и тремя нейронами классифицировать. Например, так (вообще, на картинке выше – 369 эпох, но и 200 эпох будет достаточно):
history = model.fit(X_train, y_train, epochs=200, batch_size=10, validation_split=0.2, verbose=1)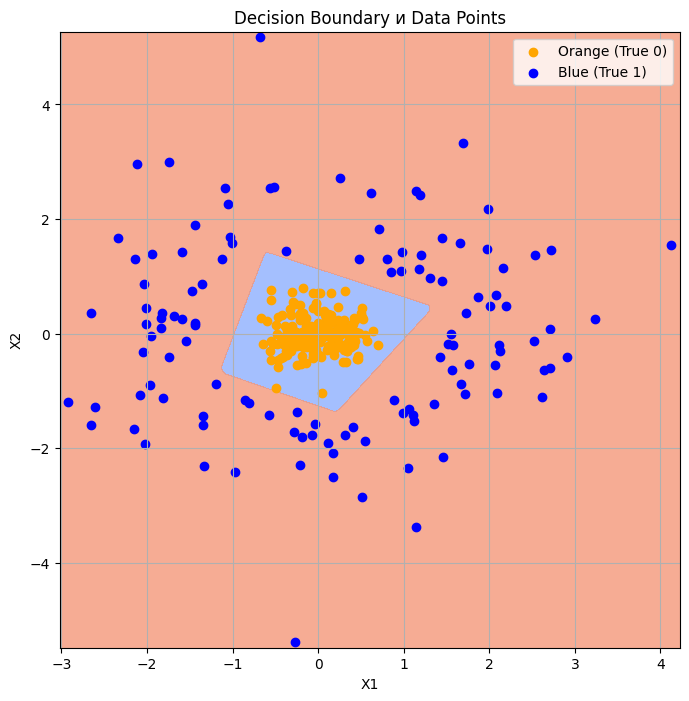
В наших примерах, мы также будем использовать наборы данных из оранжевых и голубых точек. Но мы не будем стремиться к минимальному числу нейронов, а лишь к примерно одинаково хорошим результатам предсказаний модели.
Генерация данных
Google Colab здесь. В этом файле – весь код, все вычисления: генерация, тренировка, предсказания и графики. Файл поделен на 4 части. Они свернуты в заголовки.
Данные при генерации сохраняются в CSV-файл (circle_classification_separable_dataset.csv). Код генератора прокомментирован и достаточно простой, поэтому я просто сразу приведу график сгенерированных данных (для 1000 точек):
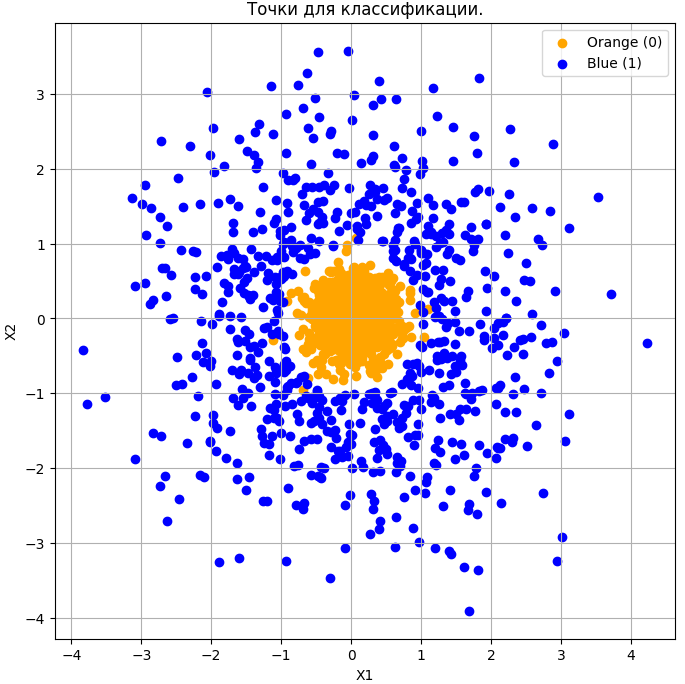
Итак, целью классификации является угадывание нейросетью цвета точки в зависимости от координат.
Классификация данных нейросетью
Нейросеть, в отличии от моделей SVC и Decision Tree, задается не одной командой и имеет ряд параметров, начиная от количества нейронов, заканчивая параметрами компиляции.
Код код классификации также доступен по ссылке, приведенной выше. Сеть последовательная с одним слоем из 8 нейронов. Выходной слой данной нейронной сети должен иметь один нейрон и подходящую функцию активации для бинарной классификации – это sigmoid. На вход подается две фичи (координаты точки X1 и X2), поэтому форма входа декларируется, как shape=(2,):
model = tf.keras.models.Sequential([
tf.keras.layers.Input(shape=(2,)), # Input shape задана отдельно
tf.keras.layers.Dense(8, activation='relu'), # 1й hidden layer
tf.keras.layers.Dense(1, activation='sigmoid') # Выходной слой для бинарной классификации
])Компиляция модели
Немного о параметрах оптимизации. Они определяются при компиляции модели:
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])-
Optimizer = 'adam': Адаптивный оптимизатор подходит для задач общего характера (не имеющих выраженной специфики – обучение с подкреплением, ограничения, более сложные архитектуры сети), часто применяется в бинарной классификации. -
loss = 'binary_crossentropy': То как вычисляется ошибка при обучении сети. Формула есть с логарифмами. Функция Sigmoid дает число между 0 и 1, которое интерпретируется, как вероятность принадлежности либо к 0 либо к 1. Поэтому ошибка считается для вероятности, а не просто “одно минус другое”. С этим также связано то, что фигурирует понятие энтропии. Стандарт для задач бинарной классификации. -
metrics = ['accuracy']: Простая в визуальном понимании метрика качества модели обученной модели на каждой эпохе. Особенно, когда оба класса одинаково важны (то есть у нас нет опасений насчет неправильного предсказания какого-то одного класса, как в задачах диагностирования заболеваний или кредитного рейтинга).
Accuracy vs Loss
При запуске тренировки модели (fit()), основанной на нейронной сети, Вы увидите, что на каждой эпохе печатается Loss и Accuracy.

fit() c параметром verbose = 1 (по-умолчанию). С параметром verbose = 0 выводится только последняя эпоха. loss – это то, “насколько” отличается выдаваемый для данного входа результат от конкретной метки, а accuracy – это процент правильных предсказаний из общего числа. Приставка val – от слова validation (data) – оценка по валидационным данным. Их доля от тренировочных определяется при запуске обучения параметром validation_split:
history = model.fit(X_train, y_train, epochs=100, batch_size=32, validation_split=0.2)Результаты работы DL модели
График тестовых данных с точными метками (сплошные кружки) и наложенных меток по результатам предсказания (окружности). Модель ошиблась там, где оранжевый кружок обведен синим или наоборот.
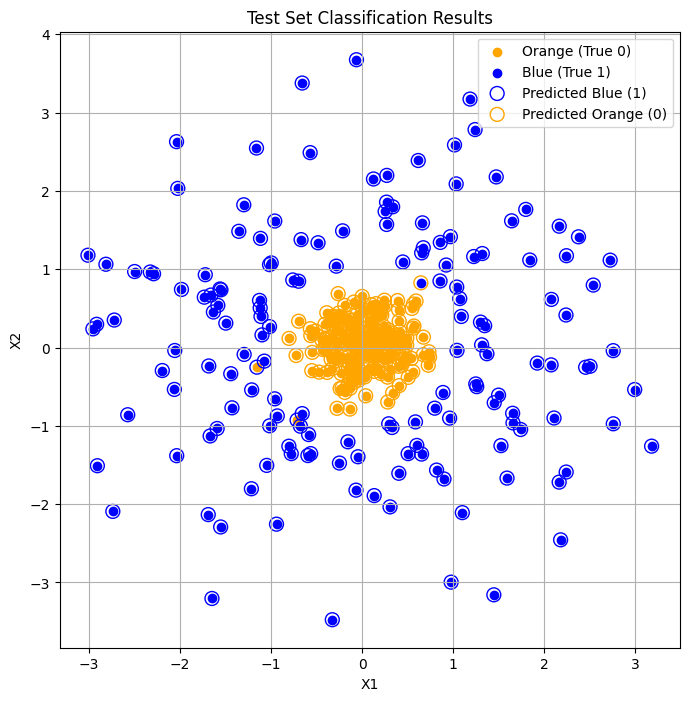
Результаты работы DL и ML моделей
Для визуальной оценки предсказания, мы можем использовать Decision Boundary, построенную по равномерной сетке в области исходных данных. В центре – серая область в которой тестовые точки отмечаются оранжевыми. Мы представим три варианта, приведем точность картинку Decision Boundary и время обучения модели. Можно заметить, что обучение моделей отличается существенно по времени.
Существует встроенная функция scikit-learn, вернее, класс для работы с Decision Boundary. У нас, в скрипте требуется работа и с DL моделью (Keras) и с ML, поэтому осталась кастомная. В кастомной функции построения plot_decision_boundary(X, y, model, resolution=100) есть два варианта построения plt.scatter(), чтобы не получилась каша из точек. При количестве точек более 5000, рекомендуется выводить на Decision Boundary каждую 20-ю точку (из исходного набора), для чего переместить комментарии в этом коде:
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='orange', label='Orange (True 0)')
#plt.scatter(X[y == 0][::20, 0], X[y == 0][::20, 1], color='orange', label='Orange (True 0)')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='blue', label='Blue (True 1)')
#plt.scatter(X[y == 1][::20, 0], X[y == 1][::20, 1], color='blue', label='Blue (True 1)')Выводы
-
При небольшом размере данных, схожих визуальных признаках правильной работы классификатора и примерно одинаковых метриках, классические ML алгоритмы по времени обучения существенно выигрывают у DL алгоритма.
-
DL модель при увеличении размера исходных данных с 1000 до 100000 так и не стала кратно увеличивать время тренировки. Время тренировки не росло пропорционально числу примеров (исходных точек). В последнем кейсе увеличение данных в 100 раз дало увеличение времени тренировки в 45 раз. В то же самое время, классические модели обе уже увеличивали время тренировки в большее число раз, чем росло число исходных данных.
-
В начале, с небольшим количеством данных (1000 точек), классические модели очень существенно выигрывали у модели DL, но с ростом количества точек, этот выигрыш может пропасть. Хотя до 100000 точек выигрыш так и не пропал. DL модель все еще была существенно медленнее в тренировке.
-
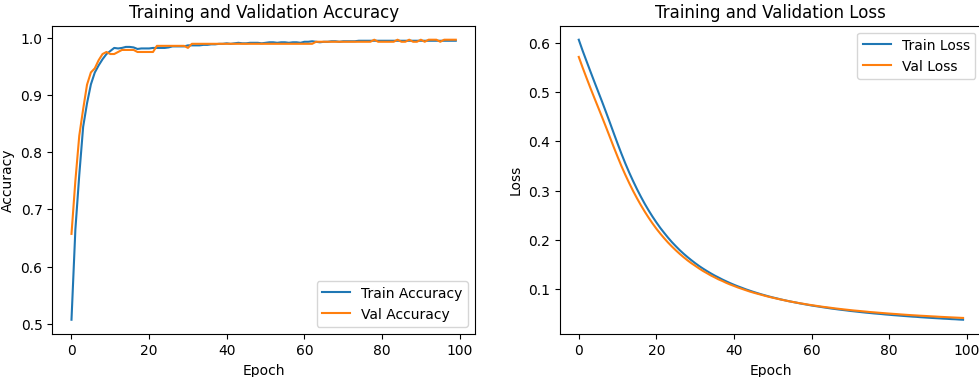
При увеличении количества семплов (точек), точность DL сходится к приемлемым значениям быстрее это видно по графикам сходимости, которые строятся в коде тренировки DL-модели Loss(Epoch).
Следует отметить еще один момент (следствие из 4-го вывода). DL модель училась все время до 100 эпох. Это во многих ситуациях не нужно, график точности Loss(Epoch) стал горизонтальным гораздо раньше в примере на 100 000 точек. Поэтому производительность обучения DL-модели на большом объеме данных может оказаться еще более выгодной и близкой к модели SVC.
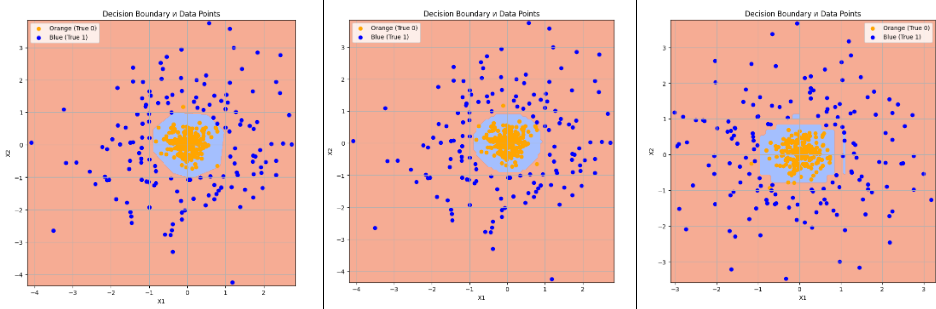
Результаты для справки
1000 точек
|
DL 8 нейронов |
Support Vector Classifier (SVC) |
Decision Tree Classifier |
|
|
|
|
|
|
|
|
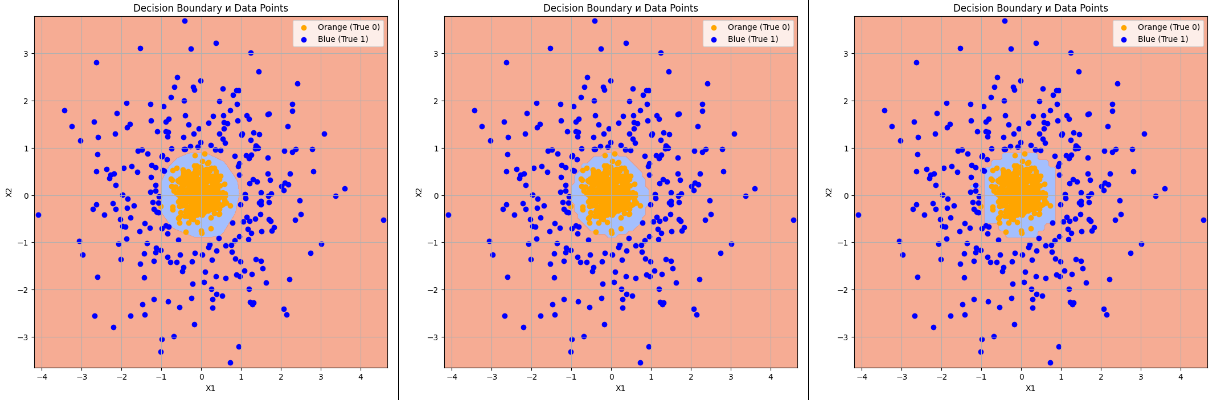
2000 точек
|
DL 8 нейронов |
Support Vector Classifier (SVC) |
Decision Tree Classifier |
|
|
|
|
|
|
|
|
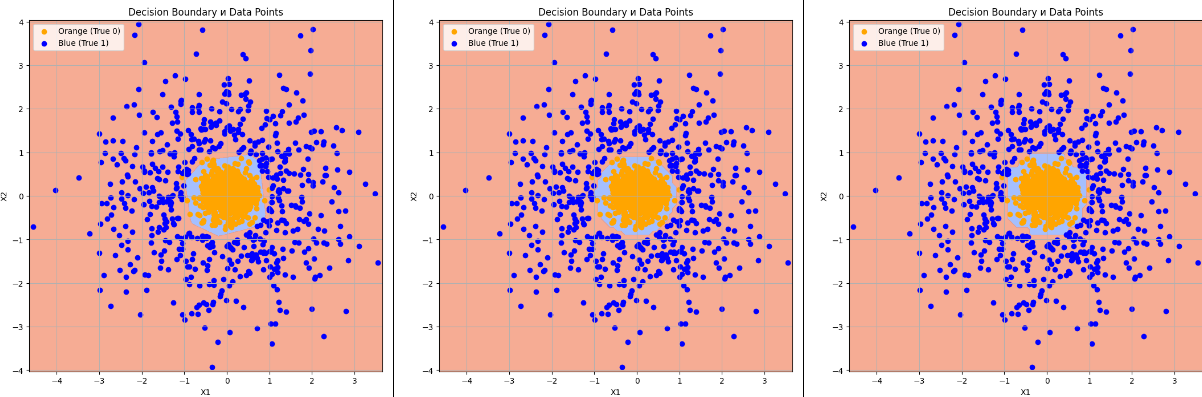
4000 точек
|
DL 8 нейронов |
Support Vector Classifier (SVC) |
Decision Tree Classifier |
|
|
|
|
|
|
|
|
100 000 точек
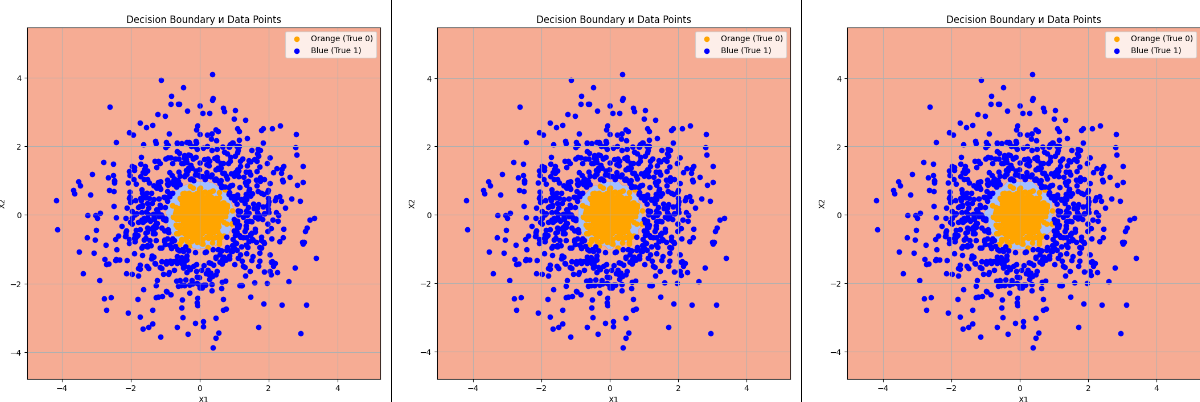
|
DL 8 нейронов |
Support Vector Classifier (SVC) |
Decision Tree Classifier |
|
|
|
|
|
|
|
|
При увеличении числа примеров в данных в 100 раз, DL модель работает в 46 раз дольше, SVC работает в 1841 раз дольше, а Decision Tree – в 135 раз дольше. Кратность времени обучения для классических моделей превысила кратность количества данных. У модели SVC она всегда была больше.
Автор: DSDenisov


