Так же как некоторое количество медуз, предоставленных самим себе, всегда образует некую формацию со стабильной повторяющейся петлей, ограниченное число нервных состояний рано или поздно образует стабильное состояние.
На рис. 25 я изобразил некоторое количество потенциальных состояний, каждое из которых представлено в виде простого кружка.
Рис. 25. Потенциальные состояния в виде кружков
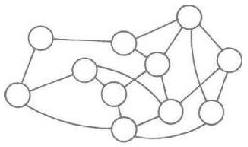
Теперь соединим кружки линиями, как показано на рис. 26. Не имеет никакого значения, как распо-лагаются эти линии, поскольку они представляют собой потенциальные переходы от одних состояний к другим. Скажем, можно было бы провести линию от каждого кружка к каждому другому кружку, но в результате получилось бы просто ненужное нагромождение линий.
Рис. 26. Потенциальные переходы от одних состояний к другим
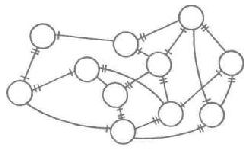
Как я указывал ранее, в каждой конкретной совокупности обстоятельств состояние «ведет к» или «сменяется» другим состоянием в единственном числе. Поэтому пометим начало одного из потенциальных переходов двумя черточками, чтобы показать, что это предпочтительный переход. Второй выбор обозначим одной черточкой. Таким образом, на рис. 27 после состояния А с гораздо большей вероятностью наступит состояние В, чем С.
Рис. 27. Вероятность наступления состояния
Рис. 28. Вероятность наступления состояния с предпочтениями
На рис. 28 к предыдущим состояниям были добавлены черточки — так мы отметили наши предпочтения. Предлагаю вам самим построить подобную диаграмму, придерживаясь такой схемы:
1. Разместите кружки на листе бумаги произвольным образом.
2. Соедините их между собой каким угодно способом (по крайней мере две линии на каждый кружок).
3. Для каждого кружка пометьте одну линию, отходящую от него, двумя черточками, а одной черточкой — любую другую линию, отходящую от этого кружка.
Я хочу подчеркнуть, что специально не придумывал расположение кружков и линий.
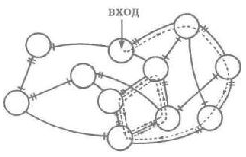
Теперь возьмите карандаш и, войдя в систему через какой-нибудь кружок, проследуйте одним из возможных путей. Вы всегда должны покидать кружок вдоль линии, помеченной двойным штрихом. Если вам случилось попасть в кружок вдоль двойной линии, вы обязаны покинуть его по линии, помеченной одиночным штрихом (это ваш второй выбор). Посмотрите, что у вас получилось.
На рис. 29 показан путь, который избрал я, и то, что из этого получилось. Совершенно очевидно, что имеется повторяющаяся петля и что все прочие состояния нестабильны и питают указанную петлю.
Рис. 29. Путь выбора состояний. Петля
Итак, мы имеем самоорганизующуюся систему, которая объясняет загадку восприятия: как мозг формирует стабильные восприятия из хаоса окружающего мира? Организация работы мозга такова, что стабильные восприятия неизбежно формируются вне зависимости от входящей информации. Стоит потокам восприятия сформироваться, и мы будем всегда видеть мир определенным образом, точно так же как в рассмотренной выше системе с воронкой мы всегда получали один и тот же результат.
Поведение самоорганизующихся систем чрезвычайно просто, если мы трактуем их как самоорганизующиеся системы. Если мы не сделаем над собой такое усилие, а будем продолжать смотреть на них по старинке, в этом случае они будут казаться нам в высшей степени сложными. Мы всегда склонны были смотреть на работу мозга по старинке.
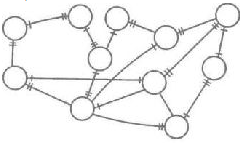
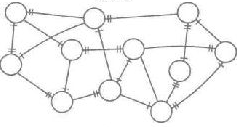
Два дополнительных примера самоорганизующихся систем представлены на рис. 30 и 31. Войдя в систему в любой точке и проследовав по предпочтительным путям, вы всегда окажетесь в стабильной повторяющейся петле.
Рис. 30. Пример 1. Выбор пути. Петля
Рис. 31. Пример 2. Выбор пути. Петля
На данном этапе можно сформулировать теорему де Боно — очень простую теорему:
ИЗ ЛЮБОЙ ТОЧКИ СИСТЕМА С ОГРАНИЧЕННЫМ ЧИСЛОМ СТАБИЛЬНЫХ СОСТОЯНИЙ И ФАКТОРОМ УСТАЛОСТИ ВСЕГДА ДОСТИГАЕТ СТАБИЛЬНОГО ПОВТОРЯЮЩЕГОСЯ ЦИКЛА.
Теорема кажется мне такой простой, что я подозреваю, она существует уже в какой-то другой форме, но если нет, тогда ее, безусловно, стоило бы здесь сформулировать. Тем не менее приложения того, что кажется очень простым, могут быть многообразными.
