Как уже отмечалось, при выявлении алгоритмов работы мозга возникают трудности. Какова же их природа? Попытаемся ответить на этот вопрос на основе рассмотрения конкретных примеров. Выше мы привели рассмотрение работы алгоритма при игре в “побеждает чет», «поиск в лабиринте» и др.
Мы рассмотрели условия эксперимента, в котором один из игроков выучивал и использовал алгоритм игры, а другой — выполнял функцию экспериментатора, стремящегося выявить алгоритм.
Воспользуемся этой игрой для дальнейшего рассмотрения возможных путей выявления алгоритмов. Представим себя в качестве исследователя, который получает большое количество данных о конкретном поведении человека, знающего и использующего алгоритм при игре «побеждает чет». Каким образом можно перейти от этих данных к выявлению правил, например приведенного нами ранее правила «бери количество предметов на единицу больше кратного»? Мы можем еще раз убедиться в том, что путем непосредственного обобщения данных эксперимента и статистической их обработки это правило выявить не удается. Однако попытаемся решить другой вопрос. Если бы мы каким-либо способом в качестве гипотезы могли сформулировать правило, можно ли экспериментально проверить, использует ли его участник игры? На этот вопрос мы получим положительный ответ. Справедливость правила можно легко доказать путем постановки специального эксперимента. Для этого нужно, используя гипотезу о существовании правила, построить предсказание о том, сколько предметов (спичек) возьмет игрок, использующий алгоритм, на следующей стадии игры, и затем сопоставить прогноз с результатами опыта. Такой ответ не решает проблемы раскрытия алгоритма, но имеет немаловажное значение.
Теперь подумаем, как же построить гипотезу. Нужно иметь набор специальных понятий типа «кратное», «больше на единицу» и др. Рассматривая определенное количество данных о поведении игрока, имея эти или подобные им понятия, можно будет строить различные гипотезы и последовательно проверять их. При этом, конечно, объем работы будет достаточно большим.
Интересно отметить, что подобным путем знаменитый ученый XVII в. Кеплер открыл общие законы движения небесных тел. Эти законы каждый раз проявлялись в форме большого многообразия конкретных численных данных. Кеплер строил гипотезы о наличии законов и затем проверял их на фактическом материале. Это не единственный путь перехода от эмпирического материала к раскрытию «порождающего» его более общего механизма, типа закона, алгоритма.
Нельзя ли сократить перебор вариантов гипотез при исследовании? Рассмотрим ряд чисел кратных двум (2, 4, 6, 8, 10, 12, 14) и шести (6, 12, 18, 24, 30). Очевидно, что общие свойства ряда сразу позволяют откинуть некоторые варианты гипотез.
Таким образом, создавая гипотезы и проверяя их экспериментально, можно выявить отдельные закономерности (правила). Для того чтобы объединить правила в структуру алгоритма и доказать их эффективность при решении задач, можно провести эксперименты специального типа. На основе гипотезы об организации алгоритма можно построить прогнозы целостного поведения игрока и сопоставить их с результатами опыта или последовательно осуществить все команды алгоритма самому и проверить, приводит ли он к выигрышу.
Итак, мы установили значение целого ряда предпосылок и этапов деятельности: 1) наличие набора абстрактных понятий, 2) возможность сокращения перебора при построении гипотез, 3) возможность экспериментальной проверки гипотез, 4) объединение отдельных правил в алгоритм, 5) проверка эффективности целостного алгоритма. Рассмотрим, как эти этапы деятельности могут быть реализованы при изучении работы мозга, как найти систему нужных абстрактных понятий, как сократить перебор гипотез, как осуществить проверку гипотез. При анализе примера игры в «побеждает чет» такие понятия имелись у человека ранее. При изучении работы мозга их, казалось бы, нужно было еще специально выработать. Однако внимательный анализ привел ученых к выводу о том, что существенные предпосылки для решения проблемы фактически уже созданы.
Мы уже говорили о более широком понимании роли учения И. П. Павлова, о тесной его связи с осуществлением начальных стадий построения абстрактной системы. Изучение работы мозга основывалось на рассмотрении абстрактных схем, отражающих взаимодействия организма и внешней среды. При этом был сформулирован ряд понятий: «условный рефлекс», «рефлекс на комплексный раздражитель», «условный тормоз» и т. д.
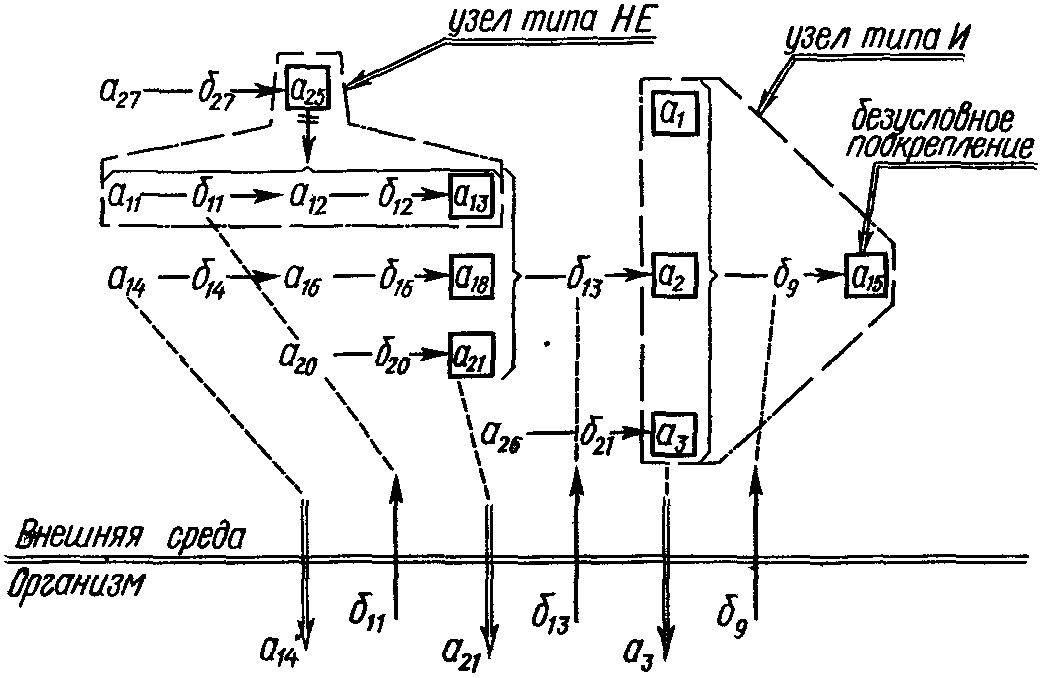
Нельзя ли использовать эти понятия при решении проблемы построения гипотез как основы раскрытия алгоритмов и затем организовать эксперименты для их проверки? Этот вопрос стал основой проведения специального исследования. Была осуществлена попытка описания отдельных компонентов алгоритмов на языке, созданном при разработке учения о высшей нервной деятельности. Для построения гипотезы осуществлялся анализ протоколов экспериментов. С целью сокращения числа возможных вариантов использовались схемы, положенные в основу экспериментов, пример которых представлен на рисунке.
Гипотеза о существовании правила должна была быть сформулирована в таком виде, который позволил бы выявить компонент работы алгоритма, применимого не только в различных ситуациях, определяемых схемой данного эксперимента, но и для различных случаев формирования поведения человека и животных в естественных условиях их жизди. Между тем результаты каждого конкретного эксперимента формулировались в виде последовательной записи возникающих в процессе опыта сигналов и действий испытуемых. Преодолеть это противоречие исследователи смогли при помощи разработанных ими новых приемов анализа, связанных с постановкой и последовательным доказательством теоретических гипотез, сформулированных на основе языка схем опыта. Эти схемы предусматривали использование таких терминов, как «рефлекс на комплексный раздражитель» (см. рисунок — а1, a2, а3), отражающий отношение взаимного дополнения элементов, условный тормоз, отражающий отношение взаи-моисключаемости элементов, понятия типа «цепи», подкрепляющие сигналы «ориентирующего», «фиксирующего типа», и т. д. На этом обобщающем языке и формулировались правила работы мозга с тем, чтобы они могли стать основой построения алгоритмов.