
Леонард Сасскинд – профессор физики в Стэнфордском университете, один из авторов теории струн, голографического принципа, гипотезы ER=EPR и космологической интерпретации КМ. Я решил сделать перевод статьи «Копенгаген против Эверетта, телепортация и ER=EPR», написанной по материалам лекции, которая была прочитана Сасскиндом в Институте перспективных исследований в марте 2016 г. Публикация достаточно старая, поэтому в конце я дополнил перевод новыми данными из более свежих работ. Из данной статьи вы узнаете, какие бывают типы квантовой запутанности, что такое GHZ-брана, как связана дополнительность копенгагенской и многомировой интерпретаций с комплементарностью чёрных дыр и почему решение информационного парадокса чёрных дыр также является решением проблемы измерения в квантовой механике. Напоследок мы разберёмся с принципом локальной дружественности, который был нарушен в 2019 г. тестом Белла-Вигнера. Итак, слово Леонарду Сасскинду.
Позвольте мне начать с трёх цитат известных квантовых физиков.
«Если квантовая механика вас глубоко не потрясла, значит, вы её ещё не поняли» (Нильс Бор)
[Примечение автора: Эверетту могло показаться, что Бор был недостаточно шокирован]
«У нас всегда были большие трудности с пониманием мировоззрения, которое представляет квантовая механика. По крайней мере, мне, потому что я достаточно старый человек, чтобы не дойти до того, чтобы эта идея стала для меня очевидной. Ладно, я всё ещё нервничаю из-за этого… Вы знаете, как это всегда бывает с каждой новой идеей, требуется поколение или два, чтобы стало очевидно, что нет настоящей проблемы. Я не могу определить настоящую проблему, поэтому я подозреваю, что настоящей проблемы нет, но я не уверен, что нет настоящей проблемы». (Ричард Фейнман)
«Есть надежда, что квантовая механика постепенно потеряет своё сбивающее с толку качество… Я наблюдал, как в преподавании квантовой механики, так и в её изучении, что студенты проходят через опыт… Студент начинает с изучения приёмов ремесла. Он учится, как делать расчёты в квантовой механике и получать правильные ответы…это сравнительно безболезненно. Вторая стадия наступает, когда студент начинает беспокоиться, потому что он не понимает, что он делал. Он беспокоится, потому что у него нет чёткой физической картины в голове… Затем, неожиданно, начинается третья стадия. Студент внезапно говорит себе: «Я понимаю квантовую механику», или, скорее, он говорит: «Теперь я понимаю, что понимать нечего…». Продолжительность и тяжесть второй стадии уменьшаются с годами. Каждое новое поколение студентов изучает квантовую механику легче, чем её изучали их учителя…» (Поль Дирак)
[Примечание автора: Слишком легко? Иногда я так думаю]
Есть ли проблема, как предполагает Фейнман – а затем предполагает, что её нет – а затем предполагает, что, возможно, она есть? Что же вызвало столько беспокойства и пролитых чернил? Совершенно очевидно, что речь идёт о запутанных отношениях между множеством наблюдателей и объектами их наблюдений; а именно, друг с другом и с остальной частью Вселенной. Стандартная квантовая механика – Копенгагенская квантовая механика – устроена таким образом, что требует одного внешнего наблюдателя, который не является частью системы. Он, она или оно время от времени взаимодействует с системой посредством процесса, называемого измерением, и при этом разрушает волновую функцию, отбрасывая все ветви, кроме наблюдаемой. С этой точки зрения наблюдения — это необратимые события, которые нельзя отменить. Этот метод хорошо работает на практике, но только потому, что обращение измерения обычно является слишком сложным процессом, чтобы когда-либо иметь практическое значение.
Очевидно, что Копенгагенская интерпретация не может быть последним словом. Вселенная наполнена подсистемами, любая из которых может играть роль наблюдателя. В законах квантовой механики нет места для коллапса волновой функции; единственное, что происходит, это то, что общая волновая функция эволюционирует унитарно и становится всё более и более запутанной.
Вселенная представляет собой чрезвычайно сложную сеть запутанных подсистем, и только в некотором приближении мы можем выделить определённую подсистему как НАБЛЮДАТЕЛЯ.
До недавнего времени мой взгляд на эти вещи был довольно похож на взгляд Фейнмана и, возможно, немного на взгляд Дирака; а именно: квантовая механика настолько запутана, что я даже не могу сказать, есть ли проблема, но, может быть, всё в порядке, потому что это работает. Вероятно, не так уж много пользы в размышлениях об «интерпретациях» и ещё меньше в спорах о них.
Но за последние два года я стал смотреть на это по-другому. Теперь я чувствую, что наши нынешние взгляды на квантовую механику являются предварительными; это лучшее, что мы можем сделать без гораздо более глубокого понимания её связи с гравитацией, но это не окончательно. Причина заключается в очень конкретной разработке, так называемом принципе ER=EPR. ER=EPR говорит нам, что чрезвычайно сложная сеть запутанных подсистем, которая составляет вселенную, также является чрезвычайно сложной (и технически комплексной) сетью мостов Эйнштейна-Розена. Мне кажется очевидным, что если ER=EPR истина, то это очень большое дело, и оно должно влиять на основы и интерпретацию квантовой механики.
Далее следует лекция, которую я прочитал в Институте перспективных исследований в марте 2016 года. Её цель состояла в том, чтобы указать на некоторые из вероятных концептуальных последствий ER=EPR.
Лекция состояла из трёх коротких семинаров:
-
«ER=EPR: Эверетт против Копенгагена» или «GHZ-браны»
-
«Телепортация через червоточину: ERB как ресурс»
-
«Две щели и червоточина»
Если и есть общая тема, так это то, что последние разработки в области квантовой гравитации могут рассказать нам о квантовой механике столько же, сколько и о гравитации. Рисунки в статье в основном являются оригинальными слайдами для лекции, а текст между рисунками – это то, что я объяснил устно.
1. ER=EPR: Эверетт против Копенгагена: «GHZ-браны»
Значение ER=EPR
Квантовая механика требует своего рода нелокальности, называемой запутанностью Эйнштейна-Подольского-Розена. EPR не нарушает причинность, но это, тем не менее, форма нелокальности. Это наиболее ясно видно, если представить себе попытку смоделировать квантовую механику на системе классических компьютеров. Мы предполагаем, что компьютеры распределены по всему пространству и представляют локальные степени свободы. Весь конгломерат должен вести себя так, как если бы внутри компьютеров были квантовые системы; системы, которые локальные наблюдатели могут «наблюдать», нажимая кнопки и считывая выходные данные. Компьютеры, конечно, должны будут взаимодействовать друг с другом, как если бы мы моделировали классическую физику. Но моделирование классической физики требует, чтобы компьютеры взаимодействовали только со своими локальными соседями.
Моделирование квантовой механики отличается. Оказывается, необходимо, чтобы все компьютеры были подключены к огромной центральной памяти для хранения запутанных состояний, а также к центральному генератору случайных чисел для обеспечения неопределённости. [Примечание: в этой статье термин «состояние» будет использоваться только для чистых состояний]
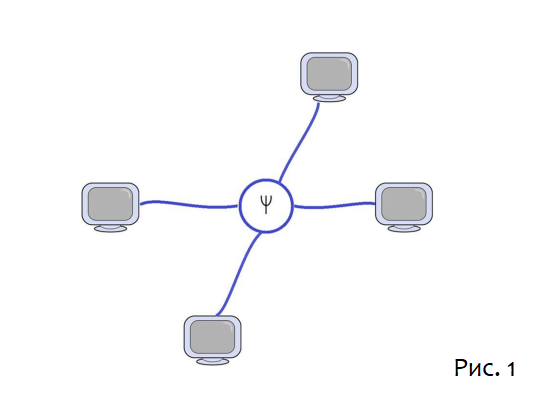
Более того, провода, которые соединяют классические компьютеры с центральной памятью, должны иметь возможность мгновенной передачи сигналов. Конечно, это не означает, что квантовая механика допускает мгновенную передачу сигналов; только то, что для моделирования КМ на классических машинах должна быть мгновенная передача. Рисунок 1 представляет собой рисунок нескольких удаленных компьютеров, подключённых к памяти, в которой хранятся запутанные состояния. На следующем рисунке пространство показано «свернутым», чтобы нарисовать пространственно удалённые точки близко друг к другу.

Две красные точки — это максимально запутанные частицы, и я указываю их запутанность, связывая их короткой черной линией. Черная связь имеет некоторую структуру; например, она различает различные максимально запутанные состояния Белла. Несмотря на видимость, нелокальные особенности запутанности не могут быть использованы для передачи сообщений сверхсветовым способом (быстрее света).
Общая теория относительности также имеет свои нелокальные особенности. В частности, существуют решения уравнений Эйнштейна, в которых пара произвольно удаленных черных дыр соединена червоточиной или мостом Эйнштейна-Розена (ERB).
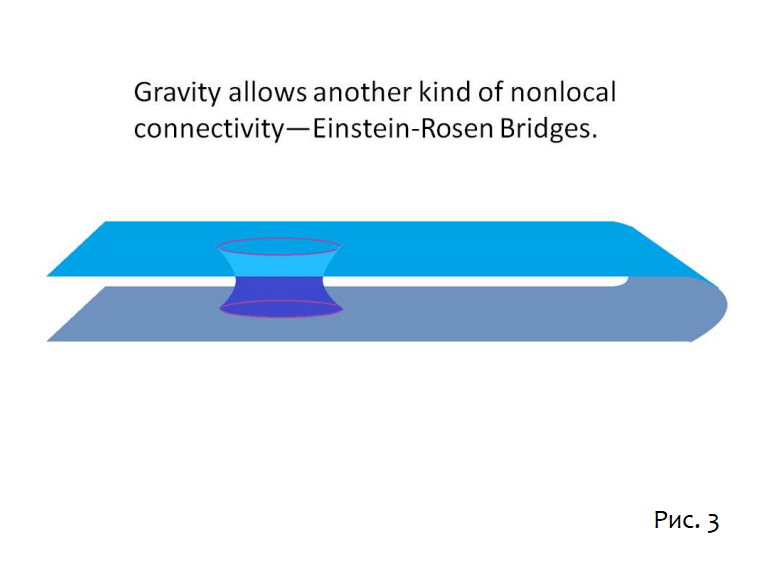
На первый взгляд может показаться, что ERB можно использовать для сверхсветовой передачи сигналов.
Но это не так; решения общей теории относительности для червоточин являются «непроходимыми». (Непроходимость означает, что два наблюдателя, находящиеся за пределами чёрных дыр, не могут общаться через ERB. Непроходимость позволяет им прыгнуть и встретиться в ERB.)
Сходство между рисунками 2 и 3 вполне преднамеренное. Кульминация шутки ER=EPR заключается в том, что в некотором смысле явления мостов Эйнштейна-Розена и запутанности Эйнштейна-Подольского-Розена на самом деле являются одним и тем же [1]:
ER=EPR.
Это замечательное утверждение, влияние которого еще предстоит оценить. Есть два взгляда на то, что это означает, один скромный и один более амбициозный. Амбициозный взгляд заключается в том, что некоторая будущая концепция квантовой геометрии даже позволит нам думать о двух запутанных спинах – паре Белла – как о связанных планковской червоточиной. Для большей части этой лекции будет достаточно более скромного определения, но ближе к концу я поразмышляю об амбициозном взгляде.
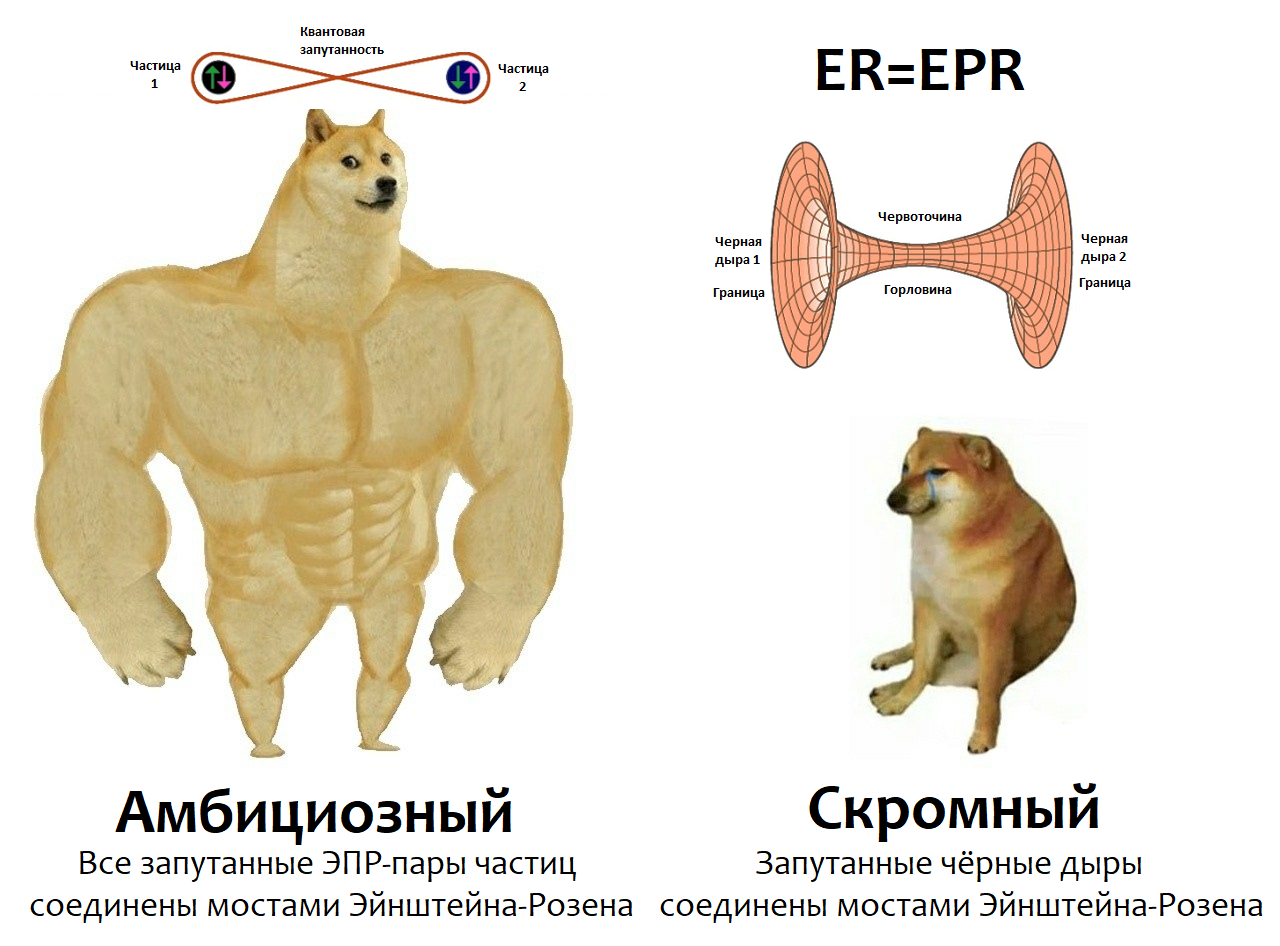
Скромный взгляд, прежде всего, говорит, что чёрные дыры, соединенные ERB, запутаны, и также наоборот; запутанные чёрные дыры соединены ERB. Но есть ещё кое-что. Идея может быть выражена в терминах запутанности как «взаимозаменяемого ресурса». Запутанность является ресурсом, потому что она полезна для выполнения определённых коммуникационных задач, таких как телепортация [2][3][4][5]. Она взаимозаменяема, потому что, как и энергия, которая существует в разных формах – электрической, механической, химической и т. д. – запутанность также существует во многих формах, которые могут быть преобразованы друг в друга. Некоторые формы запутанности:
1. Основное состояние или вакуумная запутанность;
2. Запутанные частицы;
3. Мосты Эйнштейна-Розена;
4. См. последнюю часть этой трёхчастной лекции.
А как насчет сохранения ресурса? Энергия сохраняется, а запутанность нет, за исключением особых обстоятельств. Если две системы удалены друг от друга, так что они не могут взаимодействовать, то запутанность между ними сохраняется при независимых локальных унитарных преобразованиях. Таким образом, если Алиса и Боб, которые находятся далеко друг от друга, каждый контролирует две половины запутанной системы, унитарные манипуляции, которые они делают над своими собственными долями, не могут изменить энтропию запутанности.
Если система Алисы взаимодействует с близлежащей средой, запутанность с системой Боба может быть передана среде, но пока среда остаётся на стороне Алисы и не взаимодействует с системой Боба, запутанность будет сохраняться.
Давайте рассмотрим несколько примеров преобразования запутанности из одной формы в другую. В вакууме квантовой теории поля квантовые поля в непересекающихся областях пространства запутаны. Один из способов представить это состоит в том, что виртуальные пары запутанных частиц постоянно появляются на короткие промежутки времени, как в левой части рисунка 4.

Если, как в правой части рисунка, две не запутанные реальные частицы рассеиваются на виртуальных частицах, они могут уйти в запутанном состоянии Белла.
Теперь предположим, что после создания большого количества таких пар Белла Алиса берёт половину каждой пары, а Боб берёт другую половину. Они расходятся на большое расстояние, сохраняя ресурс запутанности.
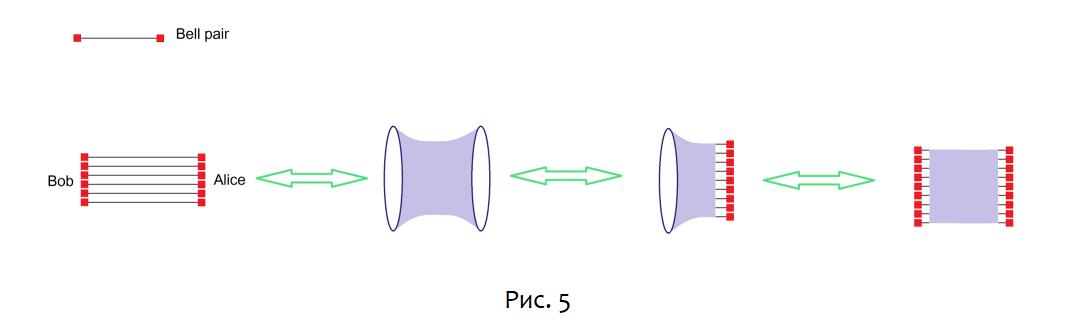
Затем каждый берёт свое облако частиц и сжимает его, образуя чёрную дыру. Согласно ER=EPR, две чёрные дыры будут соединены червоточиной. Таким образом, исходный ресурс запутанности может быть преобразован в мост Эйнштейна-Розена.
Алиса может позволить своей чёрной дыре испариться, в то время как Боб хранит свою в запечатанном отражающем ящике. Через некоторое время чёрная дыра Боба станет запутанной с облаком частиц Алисы.
Если Боб впоследствии позволит своей чёрной дыре испариться, результатом будет запутанная система частиц, которая будет настолько полностью перемешана, что будет высокая степень запутанности, независимо от того, как разделена система. С достаточно мощными квантовыми компьютерами Алиса и Боб могут локально воздействовать на свои доли, чтобы преобразовать их обратно в пары Белла.
В информационно-теоретическом смысле все эти системы – пары Белла, ERB и облака излучения Хокинга – эквивалентны и могут быть преобразованы друг в друга [6] с помощью локального унитарного преобразования, действующего независимо на концах Алисы и Боба. Хотя на практике применение таких унитарных операций может быть непрактичным, мы будем предполагать, что они в принципе возможны. Эта взаимозаменяемость позволяет нам переосмыслить квантовые явления, включающие обычные формы запутанности, в терминах геометрических свойств ERB.
Это скромное значение ER=EPR. Более авантюрный смысл заключается в том, что даже простая пара Белла имеет высококвантовую версию ERB, соединяющую её, и когда объединена с большим количеством других квантовых ERB, они сливаются, образуя большой ERB.
Копенгаген против Эверетта
Эволюция квантового состояния часто описывается как когерентное по фазе ветвящееся дерево возможностей. В Копенгагенской интерпретации наблюдатель считается находящимся вне системы, но может время от времени взаимодействовать с ней посредством процесса измерения.
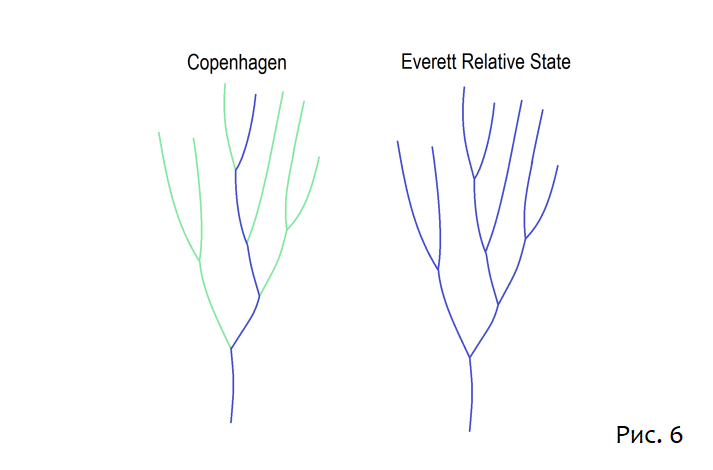
Каждое измерение приводит к декогеренции ветвей; квантовая суперпозиция заменяется классическими вероятностями. Наблюдатель следует по траектории через дерево. Согласно Копенгагенской интерпретации измерения необратимы, и относительные фазы между ветвями теряют всякий смысл.
На практике это стандартная рабочая интерпретация квантовой механики, но она не совсем последовательна. Формулировка относительного состояния Эверетта является попыткой исправить противоречивости Копенгагенской интерпретации. [Примечание: Эверетт не использовал термин «множество миров» и не любил эту идею. Метафизическая интерпретация была приписана его работе Уилером, ДеВиттом и Грэмом. Вот цитата из Стэнфордской Энциклопедии философии, которую можно найти в Интернете: «…не было консенсуса между Эвереттом, Уилером, ДеВиттом и Грэмом относительно того, что такое теория Эверетта. В частности, мы знаем, что Эверетт думал о формулировке теории Грэмом. В своей личной копии описания ДеВиттом интерпретации множественности миров Эверетт написал слово «чушь» рядом с отрывком, где ДеВитт представил разъяснение Грэмом взглядов Эверетта». Я считаю, что идеи Эверетта отражены в анализе истории о друге Вигнера, которая следует ниже]
Согласно формулировке относительного состояния Эверетта существует только одна система, Вселенная; все наблюдатели являются её частью и подчиняются унитарным законам квантовой механики. Система может быть разделена на подсистемы, каждая из которых может рассматриваться как наблюдатель. Коллапс волновой функции никогда не происходит; вместо этого взаимодействия приводят к тому, что подсистемы становятся запутанными. Всё дерево, т. е. вся волновая функция, должно быть сохранено, и Вселенная является сложной сетью запутанностей, о которой я упоминал ранее.
На самом деле дерево не является деревом [7]. В принципе всё обратимо. Например, если система замкнута, она будет выполнять квантовые повторения, в конечном итоге срастись и восстановив начальный корень. Как мы увидим, есть и другие более быстрые способы обратить наблюдения. Соответственно, относительные фазы в волновой функции всегда важны и не могут быть отброшены.
То, что на практике позволяет нам обойтись без постулата необратимого коллапса, это огромная техническая сложность обычных наблюдений, которая обычно делает невозможным их обращение.
Друг Вигнера
Чтобы проиллюстрировать два способа мышления, мы можем рассмотреть вариант эксперимента с котом Шрёдингера, «Эксперимент с другом Вигнера».
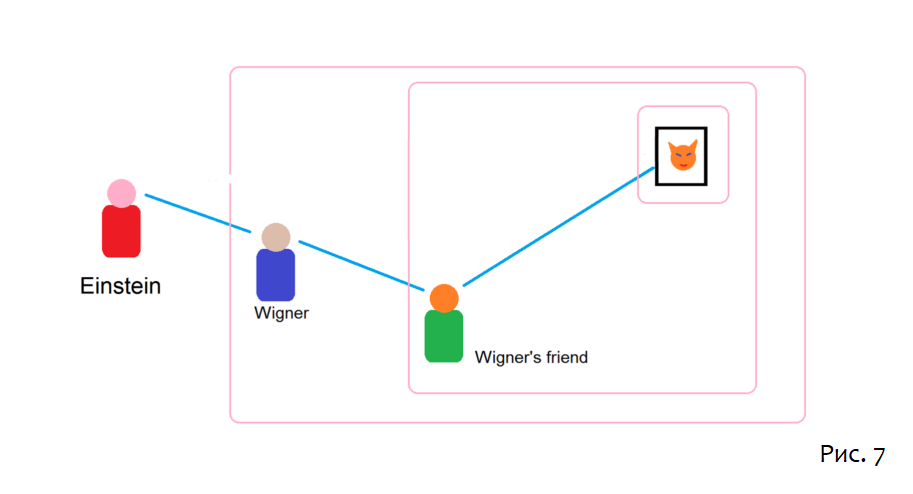
Исходный мысленный эксперимент включал двух наблюдателей: Вигнера и его друга. Мы добавим еще одного, называемого Эйнштейном. [Примечание: Почему Эйнштейн? Сначала я использовал Шрёдингера, но это так напугало кота, что он спрятался под кроватью]
Эксперимент начинается с кота в запечатанной комнате, и все три наблюдателя находятся вне комнаты. Первоначально кот в обычном состоянии кота, суперпозиции мёртвого и живого. Затем Друг Вигнера входит в комнату и наблюдает за котом. Кот, конечно, представляет собой набор N кубитов, и для наших целей наблюдение является измерением не только того, жив кот или мертв – это всего лишь один кубит, – но и всех N кубитов. Если быть точным, Друг Вигнера измеряет компонент Z всех N кубитов, т. е. всех N «Z-битов».
Чтобы записать результат, Друг Вигнера должен иметь регистр или память, в которую он классически записывает значение каждого Z-бита. Это может быть электронная память или просто часть мозга Друга Вигнера. Согласно Копенгагенской интерпретации, состояние кота коллапсирует в одно из 2N состояний, и Друг Вигнера записывает результат в свой регистр. Копенгагенская интерпретация предполагает, что нет возможности отменить измерение.
Теперь обратимся к Формулировке Относительного Состояния того же события. Вигнер может использовать такое описание до того, как войдёт в комнату, особенно если он считает своего друга и кота составляющими единую квантовую систему. В Формулировке Относительного Состояния взаимодействие Друга Вигнера с котом не вызывает коллапс волновой функции; вместо этого кубиты памяти Друга Вигнера становятся максимально запутанными с кубитами кота.
Если мы верим в амбициозную форму ER=EPR, мы могли бы сказать, что Друг Вигнера и кот становятся связанными некоторым набором квантовых червоточин. Но мы можем также обратиться к скромному взгляду; взаимозаменяемость запутанности позволяет нам сжать и Друга Вигнера, и кота в две чёрные дыры. Чёрные дыры будут запутаны, и в силу этой запутанности будет ERB, соединяющий их, как на рисунке 8.
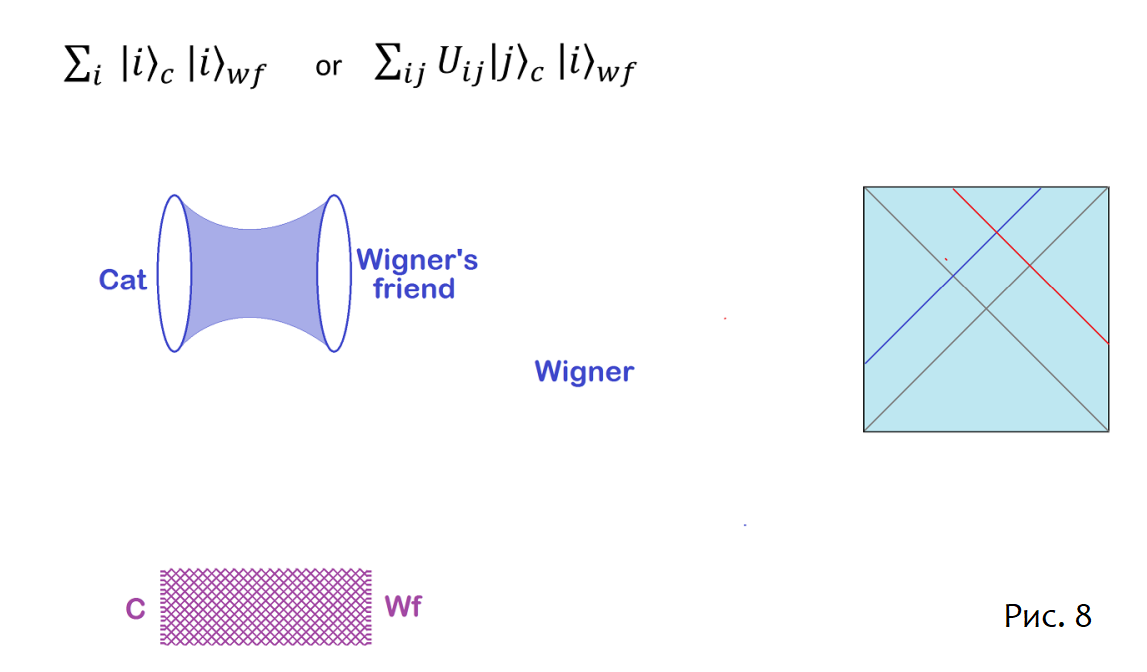
По мере развития времени после сжатия ERB будет расти, поскольку слои добавляются к тензорной сети. Эволюция представлена унитарной матрицей Uij и растущей тензорной сетью на рисунке 8. Следуя [1], мы предполагаем, что достаточно сложная операция позволит сообщениям (или наблюдателям), отправленным извне чёрных дыр, встречаться внутри ERB.
Теперь пусть Вигнер войдёт в комнату и понаблюдает за своим другом, снова в базисе Z. В Копенгагенской интерпретации наблюдение необратимо коллапсирует запутанное состояние в единственное незапутанное итоговое состояние. Можно визуализировать это как процесс «обрезки», который разрезает ERB на конце Друга Вигнера [8]
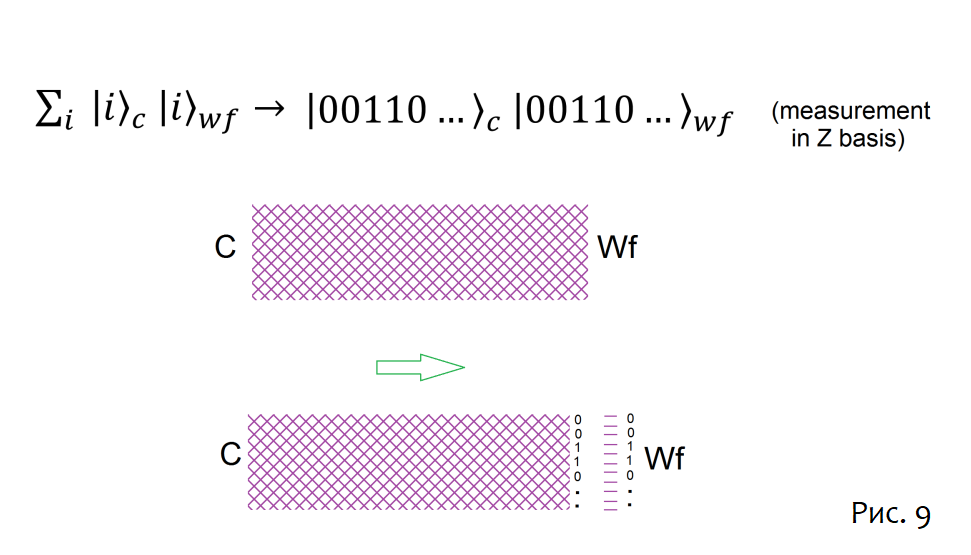
Если бы произошла какая-либо заметная эволюция ERB (рост тензорной сети), кот остался бы в довольно сложном состоянии, но Друг Вигнера, проецированный на состояние |00110…>, был бы в простом незапутанном состоянии. Очевидно, поскольку согласно Копенгагенской интерпретации, кот и Друг Вигнера больше не запутаны, сообщения с двух концов не могут встретиться в червоточине.
После того, как ERB будет разрезан, сложность двух чёрных дыр будет расти [9][10], а также объёмы двух «мостов-в-никуда». [Примечание: Односторонние чёрные дыры в чистых состояниях не имеют мостов, соединяющих их с другими системами, но у них есть растущие внутренности, которые напоминают мосты в никуда [11].] Но мост между котом и Другом Вигнера останется разрезанным до тех пор, пока две системы не будут напрямую взаимодействовать.

Эйнштейн, всё еще находясь вне комнаты и не сделав никаких наблюдений, описывает всё внутри комнаты как единую квантовую систему – кота, друга Вигнера и Вигнера. С точки зрения относительного состояния, никакого коллапса не произошло, когда Вигнер наблюдал своего друга; вместо этого они трое вошли в своего рода трёхчастное запутанное состояние, в котором кот был бы запутан с объединением Вигнера и его друга (W u WF). Эйнштейн приходит к выводу, что, когда Вигнер сжимается до чёрной дыры, должен быть ERB, соединяющий всех троих – кота, Вигнера и друга Вигнера. Он также утверждает, что сообщения с конца кота могут встречаться с сообщениями с конца W u WF, внутри ERB.

Кажется, есть явное противоречие; Копенгагенская интерпретация гласит, что никакие сообщения не могут передаваться между котом, Вигнером или Другом Вигнера. Но Эйнштейн, используя Формулировку относительного состояния, настаивает, что сообщение может быть отправлено от кота объединению Вигнера и его друга. Чтобы разрешить противоречие [8], нам нужно знать немного о трёхчастной запутанности.
Давайте упростим всё, заменив кота, Друга Вигнера и Вигнера на отдельные кубиты. Вернёмся к точке, где Друг Вигнера и кот запутаны, и Вигнер собирается провести измерение на своем друге. Вигнер начинает в состоянии |0>: Если он видит своего друга в состоянии |0>, он остаётся в состоянии |0>: Если он видит своего друга в состоянии |1> Вигнер переходит в состояние |1>: Результатом является GHZ-состояние |000> + |111>: Рисунок 12 иллюстрирует процесс.

Маленькая трёхконечная фигура — это тензорная сеть для состояния GHZ. Она обладает свойством, что она не равна нулю только в том случае, если все три внешние линии одинаковы – либо 0, либо 1: В этом случае значение тензора равно 1. Мы можем выразить его в виде,
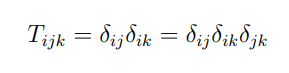
без суммы (1.1)
Если одна из трёх сторон в состоянии GHZ трассируется, две другие остаются в разделимой матрице плотности. Это означает, что матрица плотности является суммой проекционных операторов на незапутанные чистые состояния. Другими словами, никакие две стороны не запутаны, но любая одна сторона максимально запутана с объединением двух других.
Мы можем обобщить это на более сложные системы, смоделированные как наборы многих кубитов. Начнём с двух таких систем – кота и друга Вигнера – в максимально запутанном состоянии. Тем временем Вигнер (всё ещё вне комнаты) находится в состоянии |00000…>. Вигнер входит в комнату и наблюдает за своим другом в базисе Z. Каждый из кубитов в регистре Вигнера становится коррелированным с кубитом друга, таким образом производя произведение триплетов GHZ.
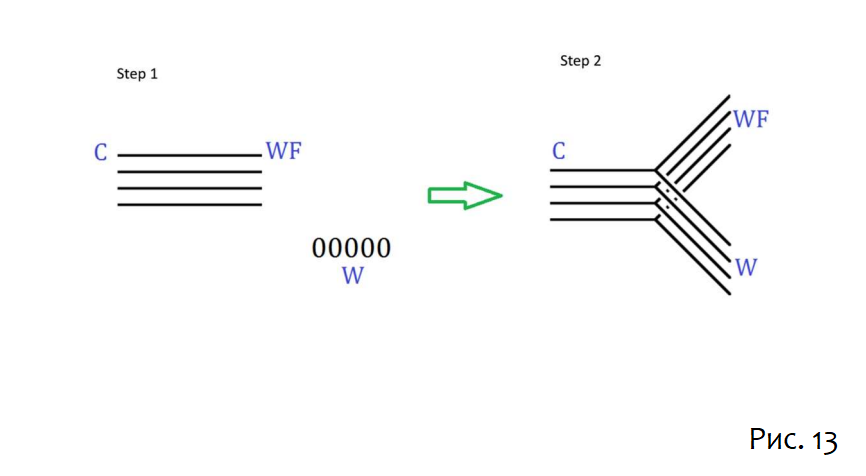
Схлопывая каждый из трёх концов, чтобы сформировать чёрные дыры и позволяя им развиваться, создаётся своего рода ERB, связывающий три стороны. Это показано как тензорная сеть на рисунке 14.
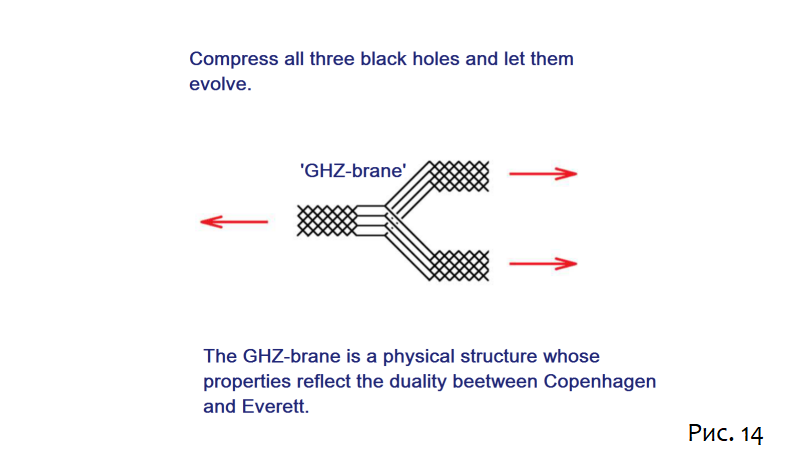
После того, как конфигурация червоточины будет создана, чёрные дыры будут развиваться и становиться всё более сложными [9][10]. Три конца трёхчастной червоточины растут линейно со временем, но независимо от того, насколько большой становится эта трёхчастная червоточина, ядро GHZ в центре никогда не исчезает. Существование максимальной запутанности GHZ является инвариантным свойством ERB.
Фигура в центре ERB представляет собой обобщённый геометрический объект, который ещё не был изучен. Его свойства отражают дуальность между Копенгагенской интерпретацией и Формулировкой относительного состояния квантовой механики. За неимением лучшего названия я назвал его GHZ-браной.
Каковы свойства GHZ-браны? Прежде всего, она локализована в червоточине. Её свойства не описываются классической геометрией, но это большой локализованный объект с дистиллируемой запутанностью GHZ порядка энтропии запутанности исходных чёрных дыр. Он обладает интересным свойством, заключающимся в том, что он не позволяет сообщениям от любых двух сторон встречаться внутри. Но поскольку любая сторона запутана с объединением двух других, если Вигнер и его друг сотрудничают, они могут совместно отправить сообщение, которое может встретить другое сообщение, отправленное котом.

Давайте рассмотрим протокол, который делает именно это. Здесь будет полезен Эйнштейн. Предположим, что когда Эйнштейн входит в комнату, он делает измерение кубитов Вигнера. Если он делает измерение в Z-базисе, он просто подтверждает наблюдение Вигнера. Это верно либо в Копенгагенской интерпретации, либо в Формулировке относительного состояния. В Формулировке относительного состояния конечное состояние кота, друга, Вигнера и Эйнштейна будет четырёхсторонним состоянием GHZ, |0000> + |1111>.
Но есть возможности, присущие квантовой механике, которые теряются в Копенгагенской интерпретации, когда мы говорим, что коллапс волновой функции необратим. Чтобы вывести эти возможности на свет, Эйнштейн делает нечто неожиданное: он измеряет кубиты Вигнера в базисе X вместо базиса Z.
Чтобы увидеть, что происходит, давайте сначала заменим все стороны отдельными кубитами. Состояния в базисе Z называются |0> и |1>. В базисе X я буду называть их |L> и |R> (для левого и правого). Игнорируя множитель √2,
|0> = |L> + |R>
|1> = |L> – |R> (1.2)
Рисунок 16 иллюстрирует анализ.

Измерение Эйнштейна может дать один из двух результатов: X = L или X = R: Интересно то, что в любом случае состояние системы кот/друг проецируется обратно в максимально запутанное состояние. Фактически, если X = L, то состояние кот/друг проецируется обратно в исходное запутанное состояние |00>+|11> (состояние до измерения Вигнера), и работа Эйнштейна выполнена.
С другой стороны, если результат X = R, то состояние кот/друг проецируется в |00>-|11>. Это состояние максимально запутано, но это не исходное состояние. Однако есть простой протокол, который Эйнштейн может применить, чтобы гарантировать, что состояние кот/друг вернется в |00> + |11>:

Если результат был X = L, Эйнштейн ничего не делает. Но если X = R, он выполняет простую унитарную операцию на Друге Вигнера, действуя с
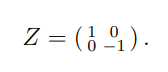
(1.3)
Это вращает состояние |00> – |11> в состояние |00> + |11>: Таким образом, независимо от того, является ли результат измерения Эйнштейна L или R, система кот/друг оказывается в исходном максимально запутанном состоянии.
Обратите внимание, что весь протокол включал действия только на Вигнере и Друге Вигнера. Кот вообще не был вовлечён. Это показывает, что совместный эксперимент на стороне Вигнера/Друга Вигнера трёхчастной системы может восстановить исходное запутанное состояние кота и Друга Вигнера.
Обобщение на множество кубитов простое и показано на рисунках 18 и 19.
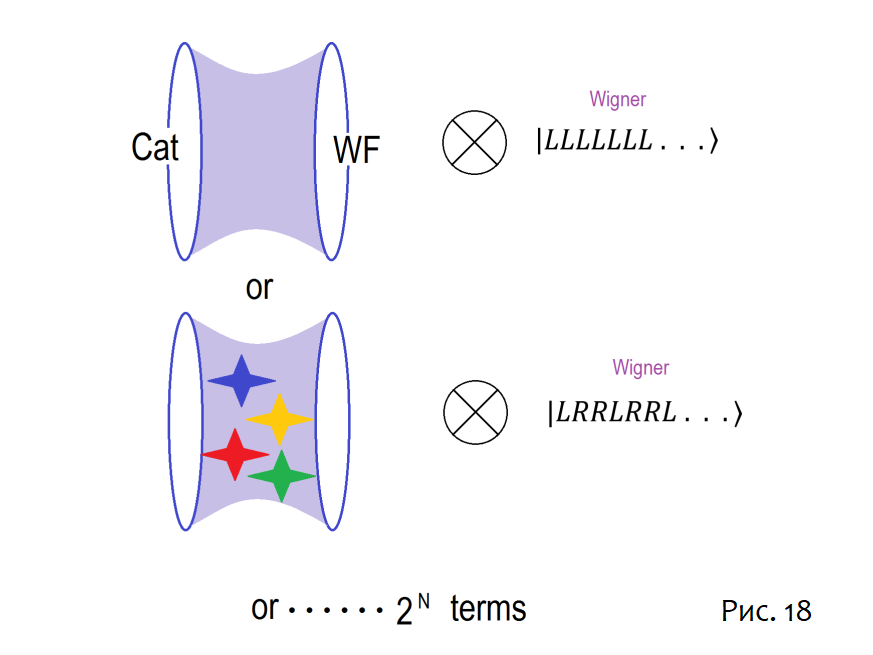
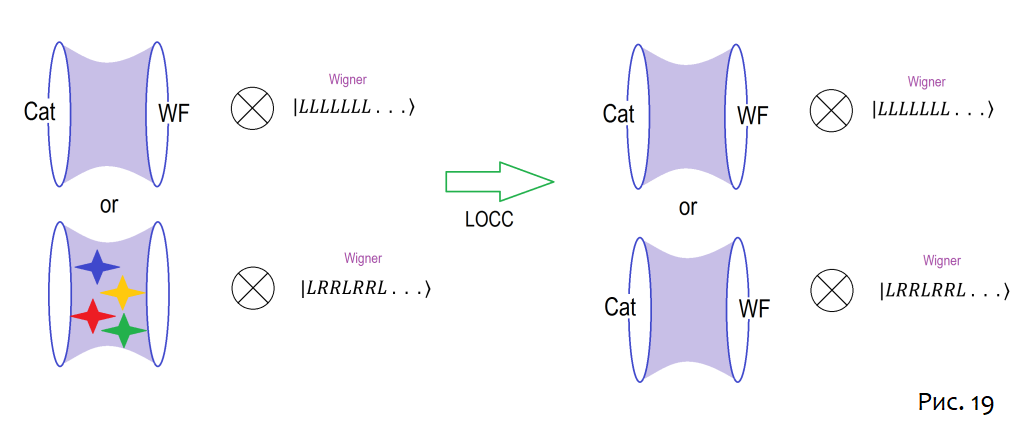
После того, как исходное запутанное состояние восстановлено, можно отправлять сообщения от кота и Друга Вигнера, которые встречаются в ERB.
УПРАЖНЕНИЕ: Вы четвёртый наблюдатель за пределами комнаты.
а) Каково ваше RSF-описание системы, состоящей из Эйнштейна, Вигнера, Друга Вигнера и Кота?
б) Если Эйнштейн также сжат до чёрной дыры, каково описание Эйнштейна, Вигнера, Друга Вигнера и кота в терминах ERB?
Брана GHZ — это новый объект, который, можно сказать, отражает дуальность между Копенгагенской интерпретацией и Формулировкой относительного состояния. Это локализованный объект в пространстве-времени за горизонтами трёх запутанных чёрных дыр. Его можно построить с помощью простой известной процедуры. Начиная с набора большого числа запутанных триплетов GHZ, общих для Алисы, Боба и Чарли, три доли сжимаются, чтобы сформировать триплет чёрных дыр. После некоторого периода эволюции внутренняя геометрия будет состоять из трёх трубчатых областей, связанных вместе браной GHZ в центре.
Количество запутанности GHZ инвариантно относительно локальных унитарных преобразований и максимально для браны GHZ. Было бы неплохо узнать, насколько запутанность GHZ присутствует в гладких классических трёхчастных червоточинах [12][13], подобных той, что показана на рисунке 11. Этот вопрос в настоящее время изучается Г. Солтоном, Б. Суинглом и М. Уолтером. Предварительный вывод заключается в том, что классические многочастные червоточины имеют очень малую или нулевую запутанность GHZ. (Похожий вывод следует из результатов [12][13].) Если это верно, то это показывает, что браны GHZ и трёхчастные червоточины с классической геометрией являются отдельными объектами, которые различимы инвариантным образом.
Общая геометрия пространства-времени GHZ-браны будет иметь структуру, показанную на рисунке 20.

2. Телепортация через червоточину: ERB как ресурс
Ранее я говорил, что ERB являются частью ресурса, но я не объяснил, как ресурс можно использовать. Во второй части лекции я покажу вам, как сложная квантовая информация может быть телепортирована через ERB [8]. Похожие идеи появились в очень интересной недавней статье Нумасавы, Шибы, Такаянаги и Ватанабе [14], а также в более ранней работе Марольфа и Уолла [15].
Цель телепортации не в том, чтобы передавать информацию быстрее скорости света; это, конечно, невозможно. Цель состоит в том, чтобы передавать информацию таким образом, чтобы никто не позволил её перехватить и восстановить то, что было телепортировано.
Начнём с того, что Алиса и Боб контролируют две не запутанные, но похожие чёрные дыры, A и B: Мы предполагаем, что Алиса и Боб находятся очень далеко друг от друга.
Кроме того, есть третья система, показанная как причудливая красная C на рисунке 21.
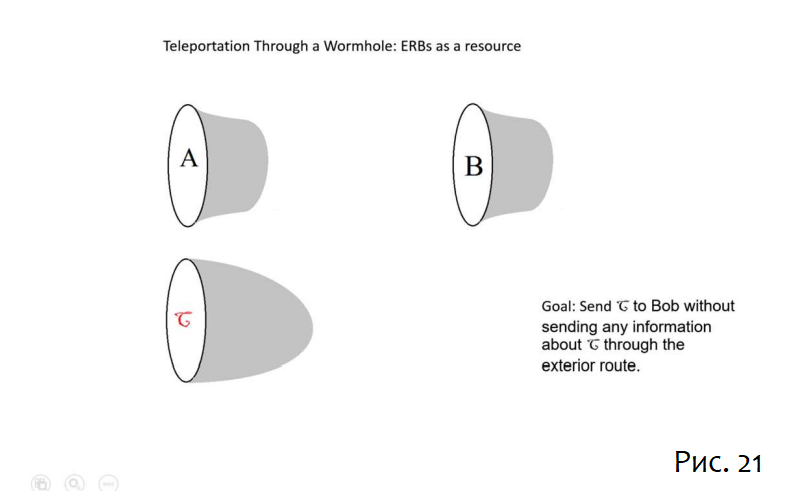
На рисунке C изображена как ещё одна чёрная дыра того же размера, что и A и B; но она может быть чем угодно, если только её информационное содержание не больше, чем у A и B: Цель Алисы – отправить квантовое состояние C так, чтобы его нельзя было перехватить. Конечно, она может просто отправить C в B; но в этом случае, если сообщение будет перехвачено, вор сможет узнать о C:
На самом деле, Алиса не сможет достичь своей цели, если она и Боб не разделят достаточно большой ресурс запутанности. Предположим, что они действительно разделяют такой ресурс в форме ERB, соединяющего чёрные дыры.
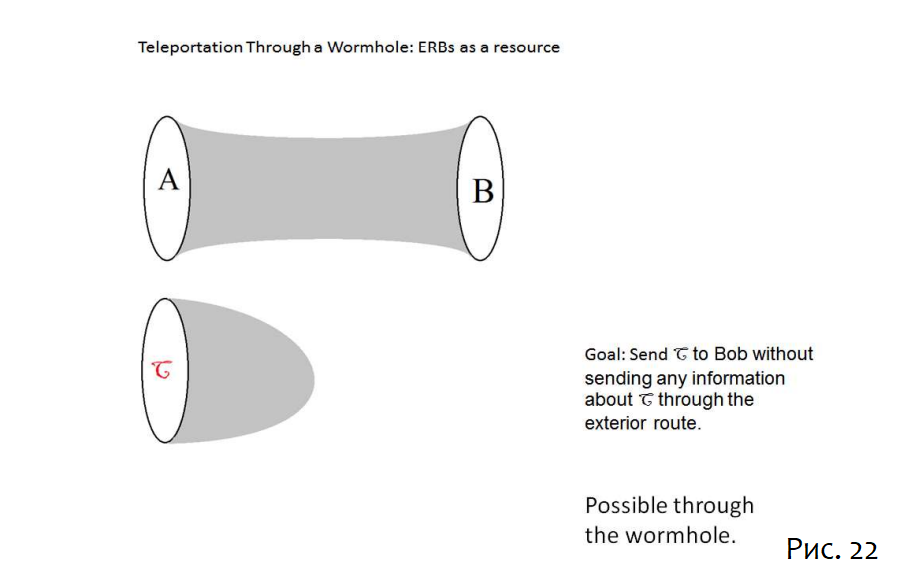
Я опишу протокол, не доказывая, что он работает. Анализ можно найти в [8]. Первый шаг — бросить C в A, чтобы сформировать чёрную дыру с удвоенной информацией в C:
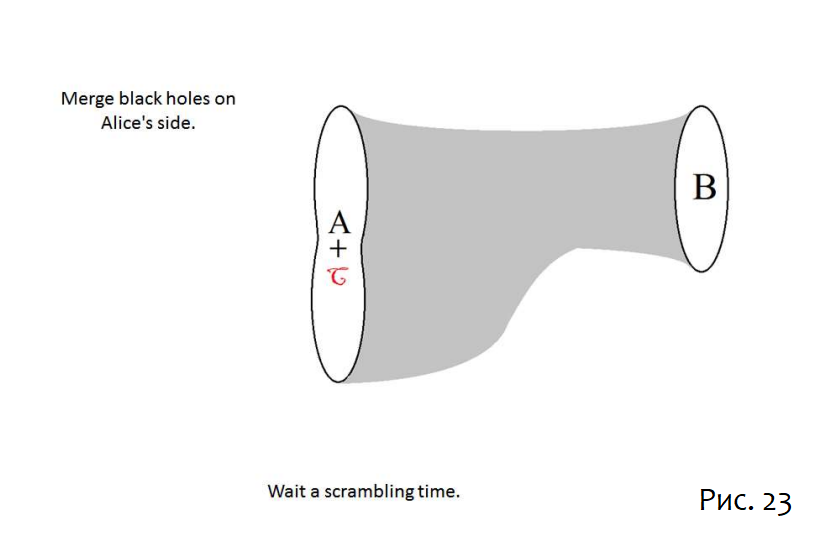
Затем подождать время скремблирования [16][17], чтобы информация в C и A была тщательно перемешана. После того, как информация в C и A будет перемешана, Алиса делает полное измерение – скажем, в базисе Z – всех кубитов, составляющих её новую черную дыру. Это отрезает её чёрную дыру и оставляет информацию C за горизонтом Боба.
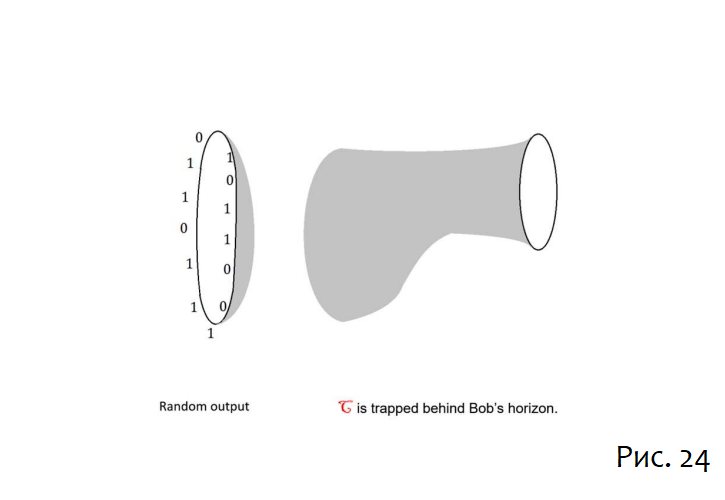
Результат измерения Алисы — это набор классических битов, которые она может записать в свой блокнот. Важным моментом является то, что классическое сообщение в блокноте Алисы совершенно не коррелирует с информацией, изначально переносимой C: эта независимость является результатом скремблирования.
Далее Алиса отправляет свой блокнот Бобу.

Конечно, это занимает время; мы не пытаемся отправить C быстрее света, только чтобы доставить C Бобу без возможности перехвата.
Теперь наступает сложная часть протокола. Когда Боб открывает блокнот, он выполняет операцию над своей чёрной дырой, которая зависит от того, что он читает. Если блокнот содержит 000000000000… он ничего не делает. Если блокнот содержит 0011101001010… он применяет определённое унитарное вращение к кубитам, составляющим его чёрную дыру. Если Боб выполнит это правильно, то он обнаружит, что состояние его чёрной дыры было преобразовано в исходное состояние C:
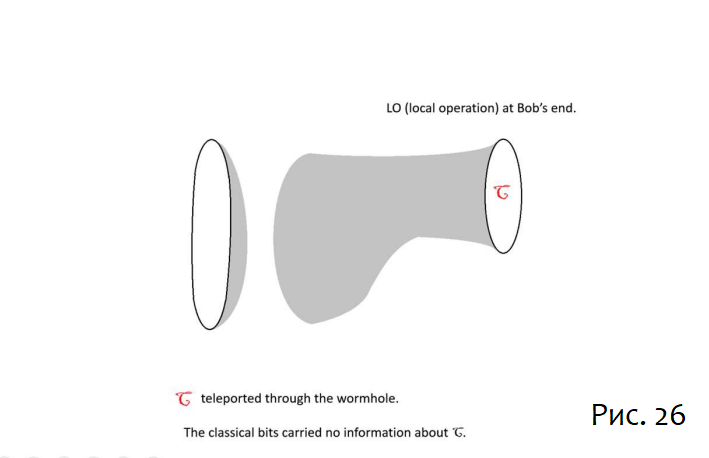
Вот ещё одна картинка, иллюстрирующая телепортацию C:
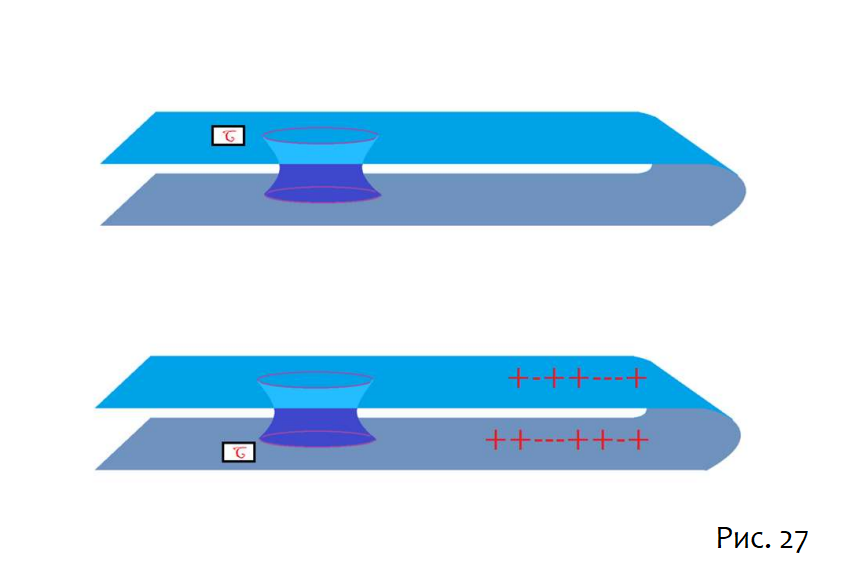
Удивительно не то, что C было отправлено мгновенно (это не так), а то, что классическая битовая строка, которая прошла «длинный путь», не несла никакой информации о C. Эта информация прошла через червоточину.
Можно сказать, что здесь нет ничего нового; это просто обычная квантовая телепортация [2][3]. Действительно, это так, но это упускает суть. Предположим, что после успешной телепортации C Алиса и Боб приходят к выводу, что должна быть червоточина, соединяющая их чёрные дыры. Боб отправляет Алисе классическое сообщение, сообщая ей, что он прыгнет в свою чёрную дыру, если она прыгнет в свою. При соответствующей подготовке они встретятся и действительно обнаружат, что чёрные дыры соединены мостом Эйнштейна-Розена. Существует корреляция: нет моста – нет телепортации.
3. Две щели и червоточина
Одни скажут, что суть квантовой механики — запутанность. Другие скажут, что это интерференция амплитуд вероятностей, примером чего является эксперимент с двумя щелями. Позвольте мне привести аргумент соломенного чучела, что это совершенно разные вещи – интерференция и запутанность. Интерференция — это явление одной частицы. Она может быть проявлена независимыми частицами, которые посылаются через аппарат по одной за раз. Интервал времени между ними может быть сколь угодно большим, и они могут исходить из разных источников, которые никогда не взаимодействовали. Запутанность, напротив, — это многочастичное явление, которое касается частиц, которые происходят из общего источника. Как следствие, нельзя ожидать, что явления интерференции будут иметь какое-либо отношение к ER=EPR.
Это неверно, и чтобы понять, почему, рассмотрим отдельную частицу (пусть для определённости это будет фермион) в суперпозиции состояний, состоящих из двух неперекрывающихся волновых пакетов с относительной фазой. Пакеты могут быть результатом прохождения частицы через две щели или полупрозрачное зеркало. Например, на рисунке 28 я нарисовал волновую функцию, состоящую из двух неперекрывающихся пакетов с противоположным знаком. Мы можем предположить, что они приближаются друг к другу и вскоре перекроются.
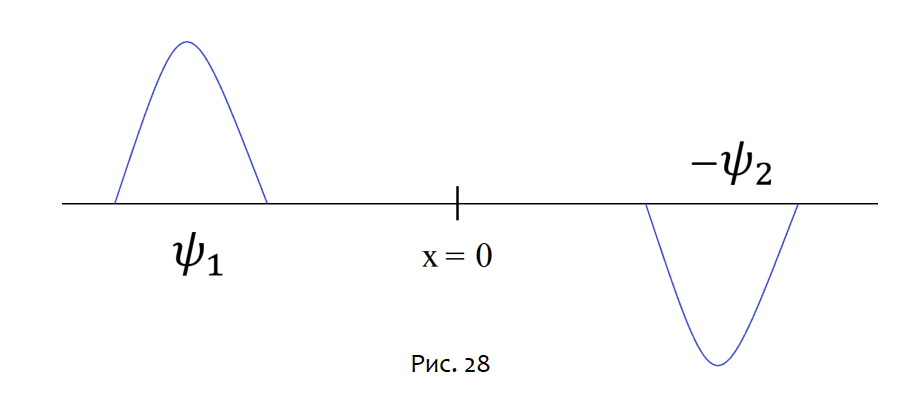
Если мы позволим волновой функции эволюционировать, то в точках деструктивной интерференции будут узлы. Любой волновой пакет сам по себе позволит частице появиться в этих точках, но разрешение обоих способов попасть туда запретит частице появиться в узле.
С точки зрения классической частицы это странно. В эксперименте с двумя щелями это приводит к вопросам типа: «как частица, проходящая через одну щель, узнала, что другая щель открыта?» Ответ, который мы узнаем в курсе квантовой механики, — квантовая интерференция.
Вместо того, чтобы сосредоточиться на частице в приведённом выше примере, давайте используем вторичное квантование и сосредоточимся на степенях свободы в двух пространственных ящиках, показанных на рисунке 29. Каждый ящик содержит один из пакетов.
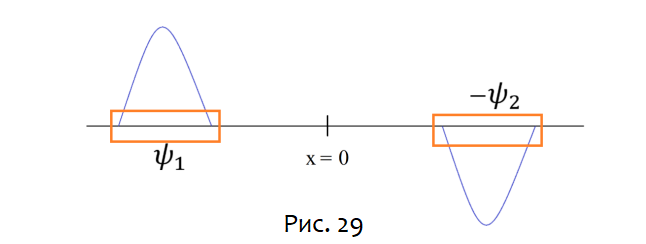
Состояние, представленное волновой функцией ψ1 – ψ2, можно переформулировать как
|10> – |01> (3.1)
где |10> представляет одну частицу в левом ящике, ни одной частицы в правом ящике; а |01> представляет ни одной частицы в левом ящике, одну частицу в правом ящике. Из формулы 3.1 очевидно, что квантовые поля в двух ящиках являются максимально запутанными кубитами. Если сосредоточить внимание на ящиках, состояние имеет форму пары Белла.
Теперь давайте предположим, что существует амбициозная версия ER=EPR. Предположим, что ER=EPR выполняется вплоть до уровня одной пары Белла. Если это можно сделать точным, два ящика на рисунке 29 будут связаны планковским ERB. Более того, когда два волновых пакета приближаются друг к другу, ERB будет следовать за волновыми пакетами, «напоминая» каждому волновому пакету, что другой есть. Состояние ERB будет отражать относительную фазу; например, были ли пакеты добавлены со знаком плюс или минус.
Очевидно, что нелокальная особенность квантовой механики, которую мы обычно называем интерференцией, может быть частным случаем нелокальности запутанности. Если мы верим в амбициозную форму ER=EPR, это подразумевает наличие моста Эйнштейна-Розена, соединяющего суперпозиции волновых пакетов для одной частицы. Свойства ERB отражают тип интерференции, т. е. деструктивную или конструктивную.
Есть ли эксперимент, который может подтвердить существование ERB в экспериментах по интерференции? Для этого рассмотрим состояние частицы сразу после того, как она прошла через 2-щелевой аппарат. Она будет находиться в суперпозиции двух пакетов, представляющих пути через две щели.
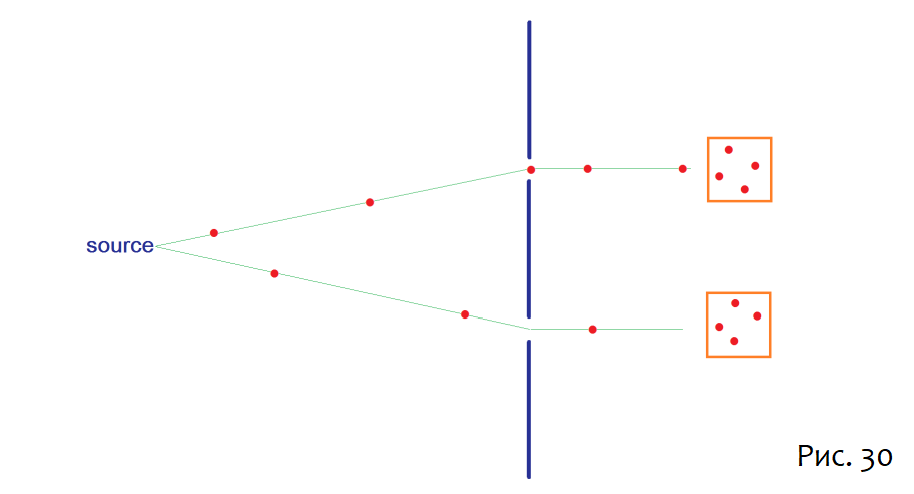
Если мы соберём много таких частиц в двух ящиках, а затем сожмём содержимое ящиков, чтобы сформировать пару чёрных дыр, мы ожидаем, что они будут связаны большим ERB. В принципе Алиса и Боб могут войти в две чёрные дыры и встретиться в ERB.
УПРАЖНЕНИЕ: Рассмотрим эксперимент на рисунке 30, но с добавлением «мониторных» кубитов в верхней щели. «Мониторные» кубиты переворачиваются, если частица проходит через верхнюю щель.
Проанализируйте эксперимент с точки зрения Формулировки Относительного Состояния. Предполагая, что мониторные кубиты также сжаты в мониторную чёрную дыру, какой вид ERB получается?
Нет ничего особенного в двух щелях. Мы можем рассмотреть эксперимент с тремя щелями. Частица проходит через щели в суперпозиция трёх состояний. Вводя три ящика, состояние можно записать как
|100> + |010> + |001> (3.2)
Очевидно, что три ящика разделяют трёхчастную запутанность, но не типа GHZ. Состояние 3.2 называется W-состоянием, по какой причине я не знаю. W-запутанность отличается от GHZ. Каждый кубит снова запутан с объединением двух других, но меньше максимального. В отличие от состояния GHZ, любые два кубита запутаны, хотя и не совсем максимально.
Собирая такие частицы в три ящика и схлопывая их, можно создать трёхчастную W-запутанную систему чёрных дыр. W-запутанность должна позволять сообщениям от любых двух сторон встречаться.
Понимание геометрии трёх- и многочастичных запутанных чёрных дыр, а также их физическая интерпретация — это задача, которую стоит решить.
4. Ну и что?
То, что я сделал в этой лекции, тривиально. Я взял некоторые обычные квантовые явления и квантовые протоколы, и, применив ER=EPR, переосмыслил их в терминах геометрии мостов Эйнштейна-Розена. Не было обнаружено никаких новых явлений, кроме корреляции с тем, что видят падающие наблюдатели, и могут ли они встретиться за горизонтом ERB. Интересно то, что такой перевод вообще возможен.
Текущий источник всей мудрости, AdS/CFT, дал огромное вдохновение и знания о квантовой гравитации, но это не всё. Почему в AdS/CFT нам никогда не приходится говорить о тех вопросах, которые затрагивает Формулировка относительного состояния?
Есть причина: существование асимптотической границы. Теория создана так, что внешний «супернаблюдатель» может манипулировать CFT и проводить измерения на ней, но супернаблюдатель не является частью системы. Для целей супернаблюдателя Копенгагенская интерпретация (и коллапс волновой функции) является достаточной структурой.
Такой супернаблюдатель делает вещи простыми, но неудовлетворительными. Рано или поздно нам придется отказаться от безопасности асимптотически холодной границы и сформулировать теорию, в которой Вселенная представляет собой сильно взаимосвязанную сеть запутанных подсистем, без предпочтительного супернаблюдателя. Я ожидаю, что когда это произойдет, ER=EPR займёт свое место в качестве одного из краеугольных камней новой теории.
Всё это говорит мне, и что я хочу сказать вам, так это то, что квантовая механика и гравитация гораздо более тесно связаны, чем мы (или, по крайней мере, я) когда-либо представляли. Существенные нелокальности квантовой механики – необходимость мгновенной связи для классического моделирования запутывания – параллели нелокальных возможностей общей теории относительности: ER=EPR.
Благодарности
Я хотел бы поблагодарить Гранта Гарибяна, Санду Попеску и Ин Чжао за обсуждения некоторых материалов этой лекции. Я также благодарен Гранту Солтону, Арону Уоллу, Брайану Суинглу и Адаму Брауну за указание на ошибки и упущения в оригинальной версии. Я также хотел бы поблагодарить Институт перспективных исследований за гостеприимство. Эта работа была частично поддержана грантом Национального научного фонда 0756174 и грантом Фонда Джона Темплтона. Мнения, высказанные в этой публикации, принадлежат автору и не обязательно отражают взгляды Фонда Джона Темплтона.
Литература
[1] J. Maldacena and L. Susskind, Cool horizons for entangled black holes,” arXiv:1306.0533 [hep-th]
[2] C.H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A Peres, W. Wootters, Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels, 1993 Phys. Rev. Lett. 70, 1895.
[3] William K. Wootters, Quantum entanglement as a quantiable resource, Phil. Trans.R. Soc. Lond. A (1998) 356, 17171731
[4] Ryszard Horodecki, Pawe Horodecki, Micha Horodecki, and Karol Horodecki, Quantum entanglement, Rev. Mod. Phys. 81, 865 Published 17 June 2009
[5] Patrick Hayden, Quantum information: Entanglement as elbow grease, Nature 4744142 (02 June 2011)
[6] B. Czech, P. Hayden, N. Lashkari and B. Swingle, The Information Theoretic Interpretation of the Length of a Curve,” JHEP 1506, 157 (2015) doi:10.1007/JHEP06(2015)157, 10.1007/jhep06(2015)157 [arXiv:1410.1540 [hep-th]].
[7] R. Bousso and L. Susskind, The Multiverse Interpretation of Quantum Mechanics,” Phys. Rev. D 85, 045007 (2012) doi:10.1103/PhysRevD.85.045007 [arXiv:1105.3796 [hep-th]].
[8] L. Susskind, ER=EPR, GHZ, and the consistency of quantum measurements,” Fortsch. Phys. 64, 72 (2016) doi:10.1002/prop.201500094 [arXiv:1412.8483 [hep-th]].
[9] L. Susskind, Computational Complexity and Black Hole Horizons,” arXiv:1402.5674 [hep-th].
[10] D. Stanford and L. Susskind, Complexity and Shock Wave Geometries,” Phys. Rev. D 90, no. 12, 126007 (2014) [arXiv:1406.2678 [hep-th]].
[11] L. Susskind and Y. Zhao, Switchbacks and the Bridge to Nowhere,” arXiv:1408.2823 [hep-th].
[12] H. Gharibyan and R. F. Penna, Are entangled particles connected by wormholes? Evidence for the ER=EPR conjecture from entropy inequalities,” Phys. Rev. D 89, no. 6, 066001 (2014) doi:10.1103/PhysRevD.89.066001 [arXiv:1308.0289 [hep-th]].
[13] V. Balasubramanian, P. Hayden, A. Maloney, D. Marolf and S. F. Ross, Multiboundary Wormholes and Holographic Entanglement,” Class. Quant. Grav. 31, 185015 (2014) doi:10.1088/0264-9381/31/18/185015 [arXiv:1406.2663 [hep-th]].
[14] T. Numasawa, N. Shiba, T. Takayanagi and K. Watanabe, EPR Pairs, Local Projections and Quantum Teleportation in Holography,” arXiv:1604.01772 [hep-th].
[15] D. Marolf and A. C. Wall, Eternal Black Holes and Superselection in AdS/CFT,” Class. Quant. Grav. 30, 025001 (2013) doi:10.1088/0264-9381/30/2/025001 [arXiv:1210.3590 [hep-th]].
[16] P. Hayden and J. Preskill, Black holes as mirrors: Quantum information in random subsystems,” JHEP 0709, 120 (2007) [arXiv:0708.4025 [hep-th]].
[17] Y. Sekino and L. Susskind, Fast Scramblers,” JHEP 0810, 065 (2008) [arXiv:0808.2096 [hep-th]].
Дополнение
Леонард Сасскинд даёт геометрическое описание запутанности между тремя системами в эксперименте «Друг Вигнера» и его усложнённой версии «обратимый друг Вигнера», предложенной в 1985 г. Дэвидом Дойчем в статье «Квантовая теория как универсальная физическая теория» в качестве способа проверки предсказаний копенгагенской и многомировой интерпретаций. Эксперимент предполагает инверсию памяти друга Вигнера и повторное измерение, позволяющее узнать, произошёл ли необратимый коллапс волновой функции. Сасскинд переводит эту схему на язык чёрных дыр и червоточин. Он рассматривает систему из трёх запутанных кубитов (состояние Гринбергера-Хорна-Цайлингера) как трёхстороннюю червоточину или GHZ-брану. В этой системе каждый из кубитов (Вигнер, Друг Вигнера и кот) находится в суперпозиции противоположных состояний. Червоточина не позволяет передавать сообщения между любыми двумя кубитами, но допускает обмен информацией между одним кубитом и парой других как единым целым. На языке многомировой интерпретации GHZ-брана является мультивёрсным объектом, соединяющим шесть классических миров с двойниками наблюдателей, пронаблюдавшими противоположные результаты измерений.
Чёрнодыровая интерпретация квантовой механики
Некоторые авторы называют гипотезу Сасскинда «чёрнодыровой» интерпретацией квантовой механики (Black Hole Interpretation of Quantum Mechanics). Так, в одноимённой статье 2020 г. Бадис Идри из университета Аннабы (Алжир) пишет следующее:
«…дополнительность между локальным наблюдателем от первого лица копенгагенской интерпретации (который видит коллапс волновой функции) и глобальным наблюдателем от третьего лица многомирового формализма (который видит непосредственно когерентную линейную суперпозицию) является аналогом дополнительности между асимптотическими и падающими наблюдателями в чёрных дырах.
Таким образом, коллапс волновой функции в задаче квантового измерения является аналогом проблемы потери информации в чёрных дырах, поскольку они обе возникают в результате отслеживания недоступных степеней свободы, приводящих к смешанному состоянию.
Аналогично, комплементарность между Копенгагеном и многомировой системой гарантирует, что проблема измерения также может быть понята как эффект грубой зернистости. Вместе с взаимозаменяемостью, т. е. взаимозаменяемостью запутанности, которая позволяет нам сжимать физические системы, наблюдателей и среды в чёрные дыры и/или излучения Хокинга, проблема измерения может быть переформулирована как проблема потери информации»
«…многомировая система кажется более общей, чем Копенгагенская, потому что она охватывает другой очень важный эффект из-за сохранения обратимости и запутанности. Между Шрёдингером и котом всё ещё могут быть сообщения, отправленные, если Шрёдингер сотрудничает с Вигнером, поскольку объединение между любыми двумя сторонами в состоянии GHZ запутано с третьей стороной, и, как следствие, сообщения могут быть отправлены между объединением любых двух из них и третьей. Следовательно, две перспективы согласованы, и именно в этом смысле многомировая система является дополнительной к Копенгагену».
Итак, дополнительность интерпретаций квантовой механики аналогична принципу комплементарности чёрных дыр. Если рассматривать друга Вигнера как испаряющуюся чёрную дыру, а кота – как излучение Хокинга, разрезанный ER-мост между ними порождает файерволл, соответствующий коллапсу волновой функции и потере информации о содержимом чёрной дыры. Если же ввести в систему внешнего наблюдателя (Вигнера), для него файерволла не существует, а ER-мост превращается в GHZ-брану, соединяющую всех троих. Заменив Вигнера квантовым компьютером, собирающим излучение Хокинга и моделирующим чёрную дыру, мы получим механизм сохранения информации, который я описал в статье «Решения информационного парадокса». Более того, математический трюк с репликами чёрной дыры и её червоточин становится понятен в свете аналогии с недавно проведённым и широко обсуждаемым тестом Белла-Вигнера.
Тест Белла-Вигнера
Расширенный вариант эксперимента с четырьмя наблюдателями, известный как «друг друга Вигнера», был проведён в 2019 г. международной группой физиков под руководством Массимилиано Пройетти по схеме, предложенной в 2018 г. Кацлавом Брукнером из Венского университета. Я упоминал его в статье «Проблема квантового измерения», но не разбирал подробно. Статья Пройетти называется «Экспериментальная проверка локальной независимости от наблюдателя». В некоторых СМИ эксперимент преподносили как доказательство, что объективной реальности не существует. На самом деле этот вывод основан на предположении о непротиворечивости, согласно которому предсказания, сделанные разными наблюдателями, использующими квантовую теорию, не должны противоречить друг другу. Но быть может, объективная реальность допускает противоположные результаты измерений?
Я не буду углубляться в технические детали и подробно описывать экспериментальную установку, рассматривая все возможные связи между кубитами. Ограничимся упрощённым объяснением «на котах». Напомню, что мысленный эксперимент «друг Вигнера» иллюстрирует противоречие между уравнением унитарной эволюции изолированных квантовых систем и неунитарным правилом теории измерений – постулатом о коллапсе волновой функции. Когда друг измеряет кота, для него происходит необратимый коллапс волновой функции, в то время как для Вигнера вся лаборатория вместе с другом находится в суперпозиции, и произведенное другом измерение является обратимым. Согласно копенгагенской интерпретации, Вигнер при измерении своего друга не может отменить результат измерения другом кота, поскольку коллапс волновой функции необратим. Согласно многомировой интерпретации, измерение, произведенное другом над котом, полностью обратимо и может быть отменено Вигнером при измерении друга в другом базисе. Группа Пройетти доказала, что верна вторая гипотеза.

В эксперименте Белла-Вигнера используется обратимая схема, описанная Сасскиндом, но с двумя вигнерами, двумя лабораториями, двумя друзьями и двумя котами. И, что самое главное, коты между собой запутаны, т.е. если один мёртв, второй должен быть жив, и наоборот. На геометрическом языке это выглядит как две GHZ-браны, соединённые мостом Эйнштейна-Розена. Вигнеров (наблюдателей за наблюдателями) зовут Алиса и Боб, изолированных в лабораториях друзей (наблюдателей) – соответственно Чарли и Дебби, ну а кот в этом эксперименте фактически один, проявляющий себя живым в одной лаборатории и мёртвым в другой. Естественно, на практике вместо вигнеров использовались фотодетекторы, а вместо друзей и котов – фотонные кубиты, запутанные между собой в разных комбинациях. Алиса и Боб случайным образом выбирают одно из двух действий: измерить состояние своего друга или инвертировать лабораторию в исходное состояние, стерев результат измерения друга, и самостоятельно измерить состояние кота.
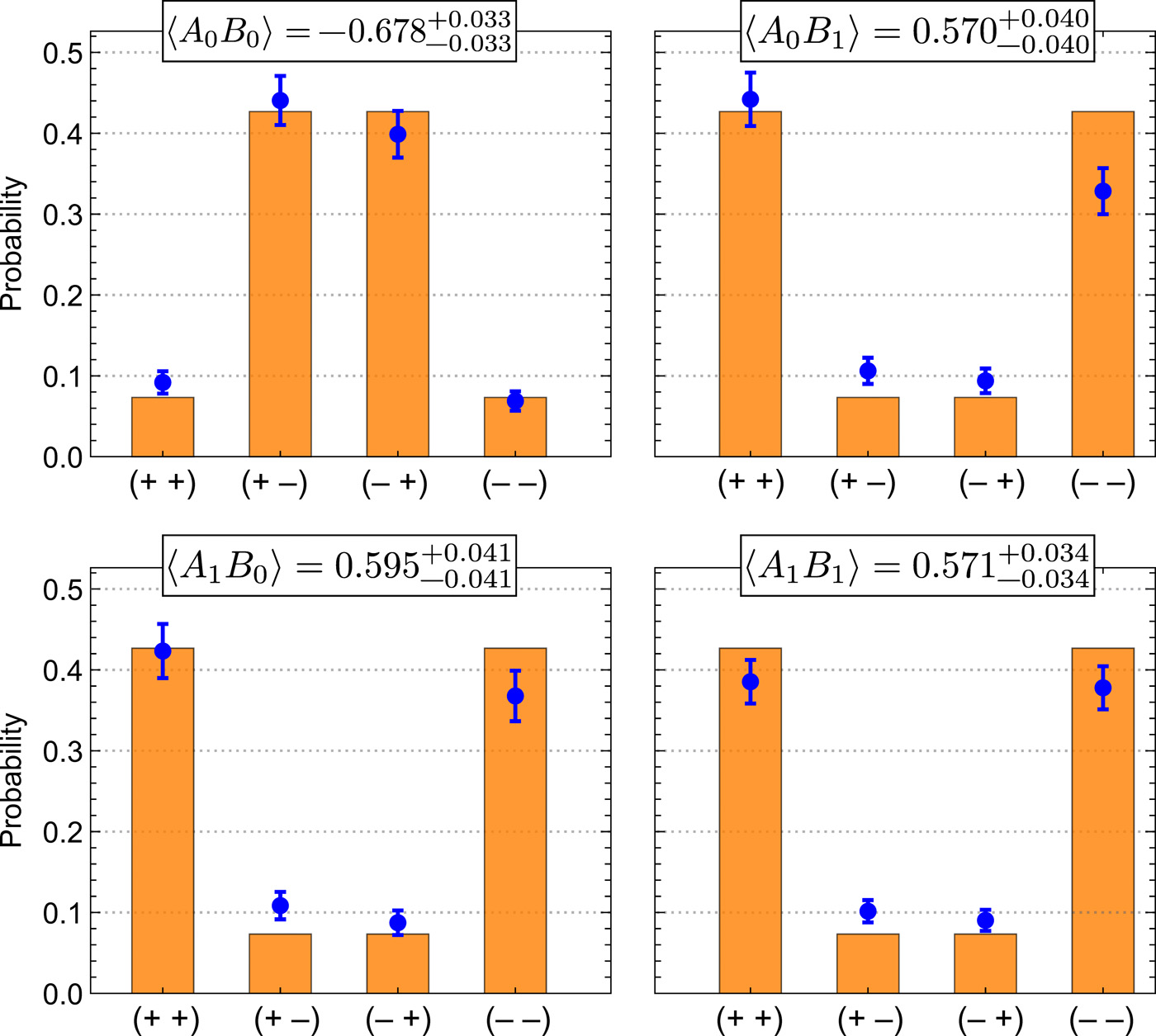
В обычном эксперименте «друг Вигнера» противоречие не очевидно, поскольку состояние кота известно только другу Вигнера и больше никому, пока Вигнер не войдёт в лабораторию. Но в расширенной версии всё обстоит иначе. Во-первых, Алиса или Боб могут узнать, совершил ли измерение друг, не зная результата этого измерения. Во-вторых, они могут отменить измерение друга, стереть ему память и измерить кота самостоятельно. Вот здесь и начинается самое интересное. В одном из 12-ти случаев наблюдения Алисы и Боба несовместимы с наблюдениями их друзей. Когда Алиса выбирает измерить Чарли, а Боб выбирает стереть память Дебби и самому измерить кота, с точки зрения Боба память Дебби будет находится в суперпозиции, а с точки зрения Алисы Дебби получит конкретный результат измерения, противоположный полученному Чарли и Алисой. И наоборот, когда Алиса выбирает стереть память Чарли и измерить кота, а Боб выбирает измерить Дебби, состояние Чарли будет неопределённым для Алисы и определённым для Боба. Но не могут же Чарли или Дебби одновременно и знать, и не знать результат измерения? Очевидно, могут. Здесь удивительно не само их пребывание в состоянии измерившего и не измерившего кота – с этим физики уже давно смирились – а в том, что состояние суперпозиции не является объективным фактом – оно зависит от наблюдателя.
Обратите внимание, что измерения Алисы и Боба всегда коррелируют, но они не смогут прийти к единому мнению по поводу результатов измерений своих друзей. Это значит, что наблюдатель может непротиворечиво описать систему только со своей точки зрения, но при описании им той же системы с точки зрения другого наблюдателя возникнет противоречие с его собственным описанием. Как же выбраться из этого порочного круга? Вариантов всего два. Первый – добавить в систему ещё одного наблюдателя за наблюдателями, который будет измерять состояния Алисы или Боба и получать только непротиворечивые результаты. Но в таком случае следует признать конечным наблюдателем вас – я обращаюсь к читателю – как единственного субъекта, в сознании которого происходит коллапс волновой функции, а остальных наблюдателей считать объектами наблюдения, чьи состояния можно обратить. Этот вариант выбирают кьюбисты и солипсисты. Второй вариант – признать объективной реальностью Мультивёрс, в котором сосуществуют противоположные результаты измерений. Его выбирают сторонники многомировой интерпретации и (немного завуалированно) сторонники реляционной интерпретации (контекстуального реализма). Также остаются в силе теории, несовместимые с квантовой механикой – супердетерминизм, нелокальная бомовская механика и теории объективного коллапса.
Теорема о запрете локальной дружественности
В статье «Сильная теорема о запрете парадокса друга Вигнера», опубликованной в 2020 г. в журнале Nature Physics, на основе анализа теста Белла-Вигнера было показано, что следующие три предположения, названные авторами «локальной дружественностью», не могут быть верны одновременно:
-
локальность (отсутствие «жуткого дальнодействия»)
-
свобода выбора (отсутствие супердетерминизма – «космического заговора», заставляющего экспериментаторов настроить детекторы так, чтобы результаты измерений создавали иллюзию нарушения неравенства Белла)
-
абсолютность наблюдаемых событий (утверждения о результатах измерений, проведенных разными наблюдателями, могут быть согласованы в рамках общей для всех наблюдателей объективной реальности).
Один из авторов статьи, Эрик Кавальканти, называет свои исследования «экспериментальной метафизикой» и сравнивает их с работой скульптора, отсекающего лишнее от глыбы мрамора: «Мне нравится представлять метафизический ландшафт как необработанный блок мрамора, где разные точки соответствуют разным физическим теориям, а об экспериментальной метафизике как о долоте, позволяющем удалять те части, которые не описывают мир нашего опыта». В этом заключается смысл современных «ресурсных» теорий и формулируемых ими «запрещающих» теорем.
Сторонники теорий скрытых параметров или объективного коллапса ожидают, когда технологии позволят провести этот эксперимент с «интеллектуальным» квантовым компьютером в роли друга Вигнера, чтобы убедиться, что волновая функция не коллапсирует в присутствии макроскопического объекта или «наблюдателя». Но в этом нет никакого смысла, поскольку квантовая теория всегда была универсальной (применимой на любых масштабах к любым объектам), а коллапс волновой функции уже давно не рассматривается как физический процесс. Для тех, кто до сих пор верит в эффект сознательного наблюдателя, в статье Пройетти специально указано:
«Отсутствие объективности возникает не в чьём-либо сознании, а между зарегистрированными фактами. Поскольку квантовая теория не проводит различий между информацией, записанной в микроскопической системе и в макроскопической системе, выводы для обоих одинаковы: записи измерений конфликтуют независимо от размера или сложности наблюдателя, который записывает их»
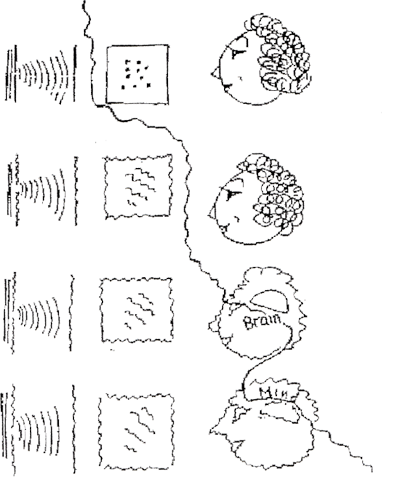
Джон Белл однажды пошутил по этому поводу: нужно ли сознательному наблюдателю иметь докторскую степень, чтобы коллапсировать волновую функцию? Также ему принадлежит рисунок, на котором изображены разные способы проведения границы между квантовой системой и наблюдателем. Очевидно, ни в одном из этих вариантов нельзя соотнести коллапс волновой функции с каким-либо физическим взаимодействием и указать его точную координату в пространстве-времени. Поэтому следует либо признать коллапс волновой функции нефизическим обновлением субъективных вероятностей, как это делают кьюбисты, либо вовсе от него отказаться, как это делают эвереттианцы. Второй вариант является более предпочтительным, поскольку описывает и самого наблюдателя как физическую систему.
Вывод
Таким образом, мы можем утверждать, что решение информационного парадокса чёрных дыр является одновременно и решением проблемы измерения в квантовой механике. Гипотеза ER=EPR, предложенная Хуаном Малдасеной и Леонардом Сасскиндом в 2013 г., стала ключом к разгадке и той, и другой проблемы. Представление любых квантовых объектов как чёрных дыр, а запутанности между ними – как червоточин, наглядно иллюстрирует причинные связи и корреляции в такой системе. Например, измерение, совершённое другом Вигнера и отменённое Вигнером, оказывается причинно изолированным от остальной системы, аналогично тому, как упавший в чёрную дыру холонавт становится причинно изолированным от остальной Вселенной. Однако для внешнего наблюдателя (Вигнера) информация полностью не теряется, просто её очень трудно воссоздать. К чему приведут дальнейшие исследования в данном направлении – сказать трудно. Но уже сейчас ясно одно: многочастичная запутанность – это мультивёрсная структура, включающая копии её элементов из параллельных вселенных. Непротиворечиво описать её в рамках одномировой интерпретации квантовой механики невозможно.
Автор: dionisdimetor


