Меня зовут Кузьма Храбров, я инженер‑исследователь в AIRI и занимаюсь задачами на стыке машинного обучения, квантовой химии и вычислительной биологии. Вместе с командой мы создаем новые датасеты, обучаем новые модели и придумываем методы решения как фундаментальных, так и практических задач.
В этом посте я расскажу про наш новый датасет малых молекул медицинской химии и бенчмарк графовых нейронных моделей, который мы собрали усилиями большой команды исследователей из групп «Глубокое обучение в науках о жизни» и «Прикладное NLP» AIRI, EPFL, СПбГУ, ИСП РАН и ПОМИ РАН. Кроме создания датасета квантовохимических свойств размером 220 терабайт, мы оценили, насколько хорошо современные нейронные модели решают задачи предсказания энергий и атомарных сил, оптимизации энергии и предсказания гамильтонианов. Наше исследование приняли на конференцию NeurIPS 2024 на трек Датасеты и Бенчмарки.
Приятного чтения!

Про электронное уравнение Шрёдингера: что это и зачем нужно
Прогнозирование свойств молекул — важный этап создания нового препарата, вещества или материала. Проверка новых гипотез в химии требует немалое количество ресурсов: синтез и дальнейшая проверка интересующих свойств конечного вещества может быть долгим и дорогим. Вместо того, чтобы проводить дорогостоящие эксперименты, некоторые свойства можно оценить с помощью методов квантовой химии.
Поведение систем на квантовом уровне подчиняется уравнению, носящему имя одного из основателей квантовой механики Эрвина Шрёдингера. Оно имеет следующий вид:
где — это волновая функция системы (ну или вектор состояния в гильбертовом пространстве, если хочется строгости),
— оператор Гамильтона (гамильтониан), который по совместительству «работает» оператором полной энергии.
Хорошая новость заключается в том, что для прогнозирования свойств молекул или материалов нам редко нужно рассматривать динамические задачи — обычно для этого достаточно знать волновые функции и энергии в стационарных состояниях. Чтобы их получить достаточно решить более простое уравнение на собственные векторы и собственные значения гамильтониана:
Такое уравнение часто называют стационарным уравнением Шрёдингера. На практике чаще всего решают именно его, а слово «стационарное» опускают. Далее по тексту мы будем придерживаться той же конвенции.
Гамильтониан молекулы включает в себя все возможные взаимодействия в системе: электронов с ядрами и друг с другом, а также взаимодействия ядер. Однако в полном виде такую задачу почти никто не решает, так как здесь на помощь приходит естественное разделение масштабов: ядерная динамика существенно медленнее электронной. Из‑за этого в квантовой химии крайне удобно использовать приближение Борна — Оппенгеймера, в котором межъядерные взаимодействия, а вместе с ними и ядерные волновые функции исключаются из задачи.
Таким образом, в волновой функции остаётся информация только об электронах. Её достаточно для того, чтобы в явном виде оценить электронные и магнитные свойства молекулы. К сожалению, для систем, содержащих два и более электронов — например атома гелия — аналитического решения не существует в принципе, поэтому приходится справляться численно. При этом объем вычислений, необходимых для решения уравнения Шрёдингера с заданной точностью, экспоненциально растет с увеличением числа электронов. Поэтому в квантовой химии применяют различные приближенные методы, которые позволяют оценить решения, демонстрируя при этом разную точностью и скоростью.
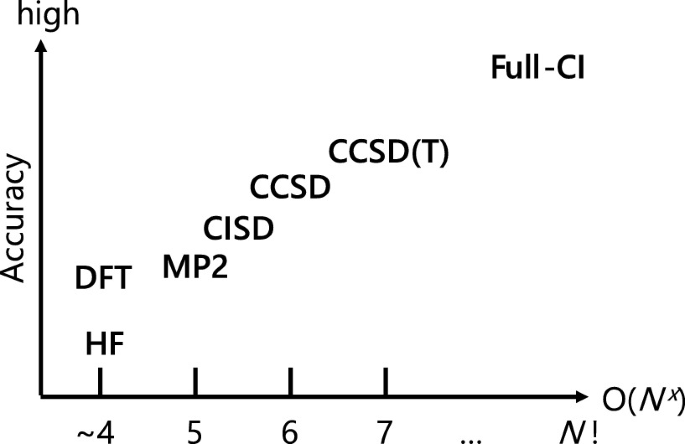
Как видно из графиков, метод на основе теории функционала плотности (density functional theory, DFT) на текущий момент является оптимальным выбором между точностью симуляции и необходимым количеством ресурсов.
Пару слов о DFT
DFT — это mean‑field метод, в котором задача многих частиц делится на несколько задач с одной частицей и который решает уравнение Шрёдингера для одного электрона в эффективном поле других электронов. Основное отличие этого метода от более точных состоит в том, что он оперирует не многочастичной волновой функцией, а электронной плотностью, которая является наблюдаемой величиной.
DFT позволяет рассматривать системы в масштабе 1000 электронов с удовлетворительной точностью (примерно 10 ккал/моль), тем самым масштабируясь до систем, которые уже являются нанообъектами, такими, как нанотрубки, кусочки белков или части каталитических поверхностей. Погрешность DFT определяется обменно‑корреляционным функционалом, который является компромиссом между точностью и сложностью. Путем подбора хорошего функционала погрешность DFT можно уменьшить до 1 ккал/моль, что сделает его одним из самых точных методов.
Несмотря на относительную простоту DFT‑похода по сравнению с более точными (Quantum Monte Carlo и Coupled Clusters), он все еще плохо применим для ежедневного расчета больших наборов молекул из‑за своей вычислительной стоимости. В связи с этим ученые начали применять модели машинного обучения для аппроксимации свойств новых структур на основе рассчитанных с его помощью.
Вычисление квантовых свойств с помощью нейросетей
Подходов в машинном обучении множество, и в последние несколько лет их так или иначе пытаются использовать в квантовой химии. Но в задаче о предсказании свойств молекул лучше всего себя показывают именно нейросетевые методы.
В статье 2017 года Neural Message Passing for Quantum Chemistry был предложен способ решения такой задачи с помощью представления молекулы в виде графа, приправленного алгоритмом передачи сообщений (message passing). Новый фреймворк позволил получить SOTA‑результаты в задаче предсказания квантовохимических свойств на датасете QM9 (если быть аккуратным, сам подход был предложен существенно раньше (например, тут), но именно в этой статье он был успешно применен к задаче молекулярного моделирования).
В дальнейшем данный подход совершенствовался, и появлялись новые архитектуры для оценки свойств молекулы (SchNet, DimeNet, PaiNN, Equiformer, NequIP, Allegro, MACE и т. д.), использующие 3D‑информацию о молекуле (координаты атомов) вместо или вместе с количеством и типом связей.
Одним из минусов применения таких подходов является необходимость учить свою модель под каждое свойство. В подобных задачах применимы методы трансферного и многозадачного обучения (transfer и muti‑task learning), но они существенно усложняют процесс.
Вместо этого можно использовать так называемый подход ab initio, когда модель предсказывает некоторое базовое свойство, из значения которого можно вычислить все интересные для исследователя величины. В качестве таких свойств могут выступать многоэлектронная волновая функция, функция электронной плотности или матрица DFT‑гамильтониана. Больше информации можно найти, например, в книге Франка Йенсена Introduction to Computational Chemistry.
Текущей SOTA здесь является подход с прямым предсказанием волновой функции методом вариационного Монте‑Карло, предложенный в работах об архитектурах FermiNet и PauliNet. Нейросетевые методы позволяют получать результаты качественно лучше классических методов, но, к сожалению, они не сильно превосходят тот же DFT по скорости применения, и при этом требуют достаточно сложного обучения.
Второй подход использует предсказание электронной плотности, но осложняется необходимостью как‑либо её представлять (например, в виде разложения по функциональному базису или с помощью графовой нейронной сети), а также сравнивать функции на решетке. Этот подход развивает несколько научных групп, например, Питер Бьорн Йоргенсен из Технического университета Дании и Цзянь Пэн из университета Иллинойса.
Наконец, третий подход сводится к аппроксимации матрицы гамильтониана, что делает задачу условно дискретной, но оставляет привязку к функциональному базису, плюс точность такого метода ограничена сверху точностью самого DFT. Первыми работами в этой области были модели SchNOrb и PhiSNet. Они позволяют получать близкие к референсным матрицы гамильтониана и значения энергии, а также ускорить сходимость DFT‑алгоритмов. Основным минусом этих подходов является применимость только к одной молекулярной формуле, то есть такие модели обобщаются только на новые геометрии той же самой молекулы.
∇²DFT — датасет и бенчмарк
Нам в нашей команде нравится подход на основе аппроксимации гамильтоновых матриц, поэтому одной из целей нашего исследования было развитие таких методов предсказания DFT. Мы создали большой датасет с разнообразными молекулами и посчитанными для них квантовохимическими свойствами, получивший название ∇2DFT (а его первая и меньшая версия называлась ∇DFT). На основе полученного датасета мы сделали бенчмарк из трех типов задач: предсказание матриц гамильтониана, предсказание энергии и атомных сил и оптимизация геометрии молекулы (конформации).
Процесс подготовки датасета состоял из 5 частей:
-
Для каждой молекулы из датасета соединений, схожих с лекарствами (MOSES), мы с помощью метода ETKDG сгенерировали до 100 пространственных геометрий (конформаций).
-
Конформации для каждой молекулы были кластеризованы по расстоянию между геометриями с помощью метода Butina. Для кластеров, покрывающих 99% всех конформаций, мы выбрали центроиды, из которых и состоит финальный датасет.
-
Для каждой из полученных геометрий мы рассчитали электронные свойства с помощью открытой квантовохимической библиотеки Psi4 методом Kohn‑Sham DFT с потенциалом ωB97X‑D и базисом def2-SVP.
-
Итоговый датасет был разделен на обучающие/тестовые подвыборки несколькими способами для исследования обобщающей способности методов. Если конкретно: обучающие выборки разного размера (2 000, 5 000, 10 000, 100 000 и 700 000), тестовые выборки конформаций тех же структур, что присутствуют в обучающих выборках, тестовая выборка молекул, не присутствующих в обучении, а так же тестовая выборка молекул, основная подструктура (scaffold) которых не встречается в обучающих выборках.
-
Для примерно 60 000 конформаций были запущены DFT‑релаксации (процессы оптимизации энергии) и сохранены полные траектории этих процессов.
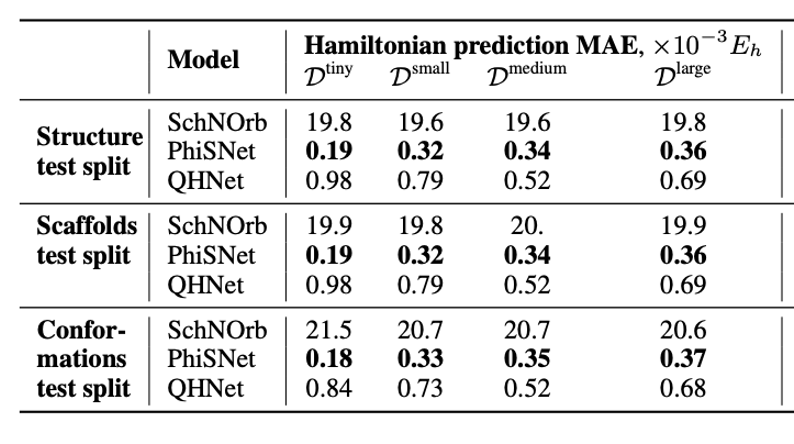
Для задачи предсказания матриц гамильтониана мы обобщили код моделей SchNOrb и PhiSNet для работы с разными молекулами и измерили их обобщающую способность. Также мы добавили сравнение с моделью QHNet, которая также адаптирована для работы с разными молекулярными структурами. Соответствующие метрики можно увидеть в табличке ниже:
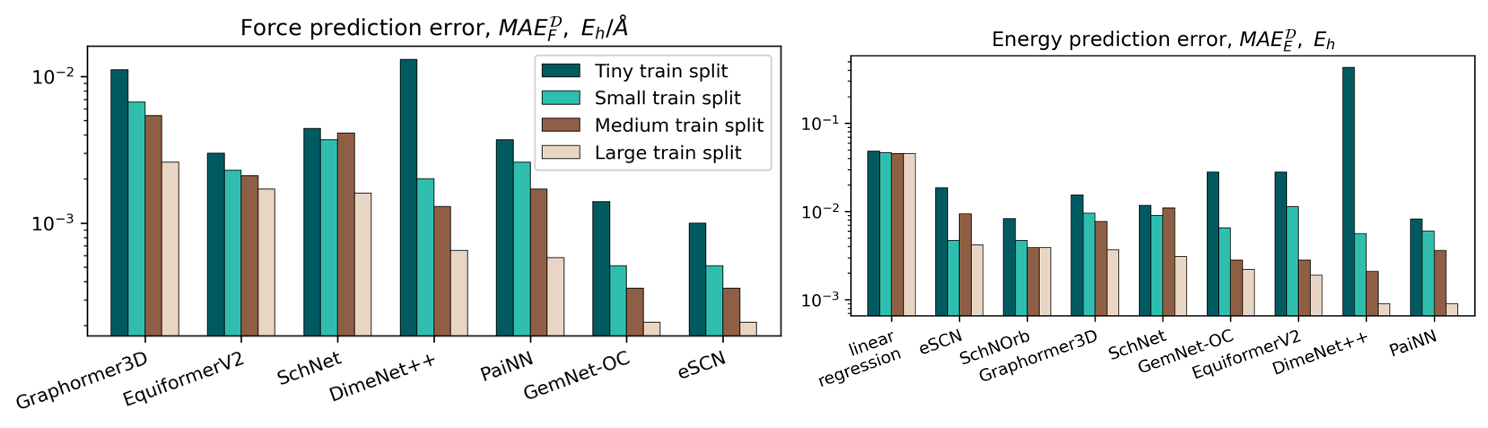
Для задачи предсказания энергий и сил мы обучили и сравнили 8 моделей на основе графовых нейронных сетей (SchNet, PaiNN, DimeNet++, Graphormer3D, EquiformerV2, eSCN и GemNet‑OC). Соответствующие метрики можно увидеть на гистограммах ниже:
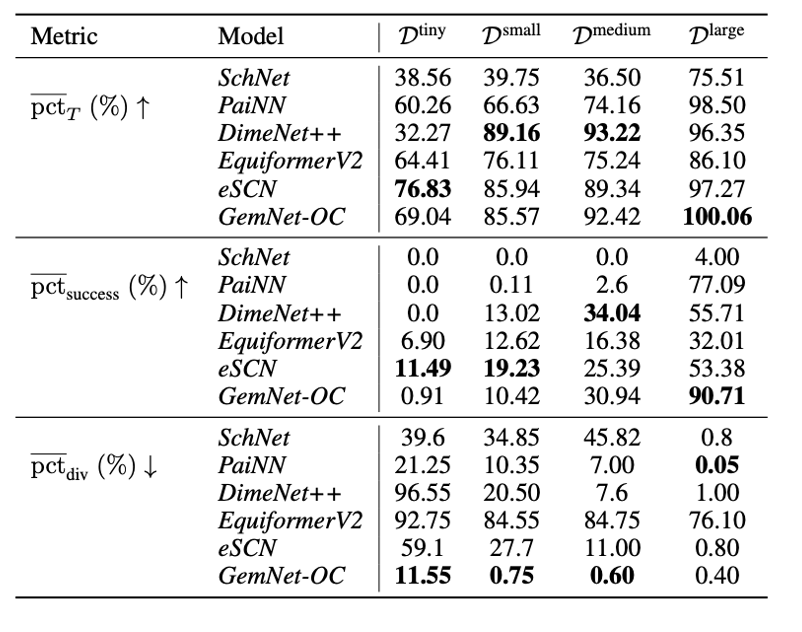
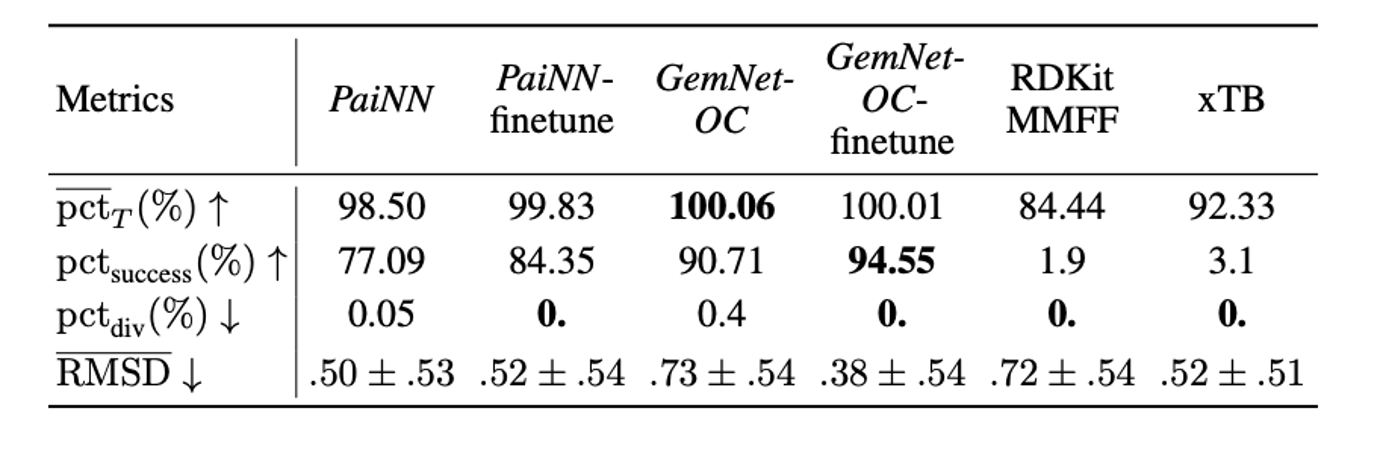
Наконец, следуя нашей статье, про которую мы уже делали пост на Хабре, мы протестировали, насколько хорошо модели для предсказаний энергий и сил могут быть применены к самостоятельному поиску оптимальных конформаций (геометрий с минимальными энергиями). Как можно видеть в табличках ниже, модели PaiNN и GemNet, обученные на больших подмножествах нашего датасета, справляются с задачей оптимизации достаточно неплохо. Кроме того, дообучение на геометриях из траекторий оптимизации приводит к дальнейшему улучшению моделей.
Итого, при поддержке коллег из Сколтеха и ПОМИ РАН мы собрали 15 716 667 конформаций для 1 936 929 подобных лекарствам молекул, а также их квантовые свойства и выложили базу данных общим размером около 220 терабайт в открытый доступ на платформу Cloud. В дополнение к данным мы включили в набор 10 моделей для предсказания энергии и атомарных сил молекулярной конформации и 3 модели для работы с теорией функционала плотности. Полный датасет и примеры работы с ним доступны через гитхаб, а результаты анализа доступны в статьях: про ∇DFT и про ∇2DFT.
Заключение
С помощью нашего датасета можно увидеть, что современные нейросетевые модели достаточно хорошо предсказывают энергии и силы — на уровне точности традиционных квантовохимических методов, а также отметить их обобщающую способность при тестировании на новых молекулах.
Но несмотря на то, что современные модели для предсказания гамильтонианов позволяют ускорить квантовохимические вычисления более чем на 3 порядка по времени, их обучение остается непростой задачей: оно требует большого количества GPU‑часов (несколько GPU‑месяцев на современных картах в случае нашего датасета), а сам процесс сильно усложняется с увеличением размера и состава молекул.
Наш проект продолжает развиваться, поэтому подписывайтесь и следите за обновлениями. Мы будем рады вашим комментариям и pull request‑ам!
Автор: KuzmaKhrabrov


